
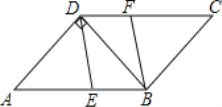
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,且
,且![]() 于点
于点![]() ,点
,点![]() 分别是边
分别是边![]() 上的动点,且
上的动点,且![]() .
.
①求证:四边形![]() 是平行四边形;
是平行四边形;
②当![]() 为何值时,四边形
为何值时,四边形![]() 是矩形?
是矩形?
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且经
,且经![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴
在抛物线的对称轴![]() 上,是否存在点
上,是否存在点![]() ,使它到点
,使它到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,如果存在求出点
的距离之和最小,如果存在求出点![]() 的坐标,如果不存在请说明理由.
的坐标,如果不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,P是⊙O外任意一点,PA、PB分别与⊙O相切与点A、B,OP与⊙O相交于点M.则点M是△PAB的( )
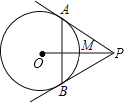
A.三条高线的交点
B.三条中线的交点
C.三个角的角平分线的交点
D.三条边的垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点P以
,动点P以![]() 的速度从A点出发,沿
的速度从A点出发,沿![]() 向C点移动,同时动点Q以
向C点移动,同时动点Q以![]() 的速度从点C出发,沿
的速度从点C出发,沿![]() 向点B移动,设P、Q两点移动的时间为t秒
向点B移动,设P、Q两点移动的时间为t秒![]() .
.

(1)t为多少时,以P、Q、C为顶点的三角形与![]() 相似?
相似?
(2)在P、Q两点移动过程中,四边形![]() 与
与![]() 的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
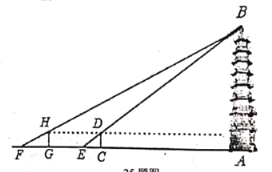
【题目】净觉寺享有“家东第一寺”的美誉,是一座规模较大,布局严颜,结构合理,独具一格的古建筑群体,被国务院批准列入第六批全国重点文物保护单位名单,某校社会实践小组为了测量寺内一古塔的高度,在地面上![]() 处垂直于地面竖立了高度为
处垂直于地面竖立了高度为![]() 米的标杆
米的标杆![]() ,这时地面上的点
,这时地面上的点![]() ,标杆的顶端点
,标杆的顶端点![]() ,古塔的塔尖点
,古塔的塔尖点![]() 正好在同一直线上,测得
正好在同一直线上,测得![]() 米,将标杆向后平移到点处,这时地面上的点
米,将标杆向后平移到点处,这时地面上的点![]() ,标杆的顶端点
,标杆的顶端点![]() ,古塔的塔尖点
,古塔的塔尖点![]() 正好在同一直线上(点
正好在同一直线上(点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 与古塔底处的点
与古塔底处的点![]() 在同一直线上)这时测得
在同一直线上)这时测得![]() 米,
米,![]() 米,请你根据以上数据,计算古塔的高度
米,请你根据以上数据,计算古塔的高度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售40件,每件盈利50元,为了减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.
(1)若某天该商品每件降价a元,当天可卖多少件?
(2)在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到2400元?
(3)每件商品降价多少元时,商场日盈利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在8×6的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.点C坐标为(2,4),以O为位似中心,在网格图中作△ABC,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹)
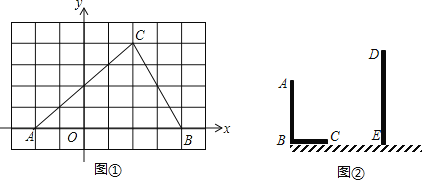
(2)则点C′的坐标为 ,周长比C△A′B′C′:C△ABC= .
(3)如图②,AB和DE是直立在地面上的两根立柱.AB=6m,某一时刻AB在阳光下的投影BC=4m,DE在阳光下的投影长为6m.
①请你在图②中画出此时DE在阳光下的投影EF.
②根据题中信息,求得立柱DE的长为 m.
查看答案和解析>>
科目:初中数学 来源: 题型:
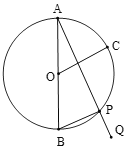
【题目】如图,AB为⊙O的直径,AB=3,弧AC的度数是![]() ,P为弧BC上一动点,延长AP到点Q,使
,P为弧BC上一动点,延长AP到点Q,使![]() .若点P由B运动到C,则点Q运动的路径长为______.
.若点P由B运动到C,则点Q运动的路径长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.

(1)求y与x的函数关系式;
(2)如果要围成面积为63m2的花圃,AB的长是多少?
(3)能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com