
【题目】如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.

(1)求y与x的函数关系式;
(2)如果要围成面积为63m2的花圃,AB的长是多少?
(3)能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
【答案】(1)y=-3x2+30x.(2)AB的长为7m.(3)能.最大面积为![]() m2.
m2.
【解析】
试题分析:本题利用矩形面积公式建立函数关系式,A:利用函数关系式在已知函数值的情况下,求自变量的值,由于是实际问题,自变量的值也要受到限制.B:利用函数关系式求函数最大值.
试题解析:(1)由题意得:
y=x(30-3x),即y=-3x2+30x.
(2)当y=63时,-3x2+30x=63.
解此方程得x1=7,x2=3.
当x=7时,30-3x=9<10,符合题意;
当x=3时,30-3x=21>10,不符合题意,舍去;
∴当AB的长为7m时,花圃的面积为63m2.
(3)能.
y=-3x2+30x=-3(x-5)2+75
而由题意:0<30-3x≤10,
即![]() ≤x<10
≤x<10
又当x>5时,y随x的增大而减小,
∴当x=![]() m时面积最大,最大面积为
m时面积最大,最大面积为![]() m2.
m2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=![]() (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为_____.
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中俄“海上联合—2014”反潜演习中,我军舰A测得潜艇C的俯角为300.位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为680,试根据以上数据求出潜艇C离开海平面的下潜深度。(结果保留整数。参考数据:sin680≈0.9,cos680≈0.4,,tan680≈2.5. ![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《丰富的图形世界》一章中,我们认识了三棱柱、四棱柱、五棱柱和六棱柱,这些棱柱是由点、线和面构成.
(1)请使用合适的方式统计上述四种棱柱顶点的个数、棱的条数和面的个数;
(2)若棱柱顶点的个数用V表示、棱的条数用E表示、面的个数用F表示,观察你的统计数据,写出V,E,F三者间的数量关系;
(3)若某几何体满足(2)的数量关系,且有24条棱和10个面,则几何体有多少个顶点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y1=(x-2)2+1与y2=x2-4x+c,过点A(1,-3)作直线l∥y轴,交抛物线y2于点B,交抛物线y1于 点C,则以下结论:
(1)抛物线y1与y轴的交点坐标为(0,1)
(2)若点D(-4,m)及点E(7,n)均在抛物线y1上,则m>n;
(3)若点B在点A的上方,则c>0;(4)若BC=2,则c=3 其中结论正确的是 ( )

A. (1)(2) B. (2)(3) C. (3)(4) D. (1)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,对角线AC,BD交于点O,AB⊥AC,AB=1,BC=![]() .
.
(1)求平行四边形ABCD的面积S□ABCD;
(2)求对角线BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
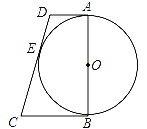
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com