练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，抛物线y1=（x-2）2+1与y2=x2-4x+c，过点A（1，-3）作直线l∥y轴，交抛物线y2于点B，交抛物线y1于 点C，则以下结论：

    （1）抛物线y1与y轴的交点坐标为（0，1）

    （2）若点D（-4，m）及点E（7，n）均在抛物线y1上，则m＞n；

    （3）若点B在点A的上方，则c＞0；（4）若BC=2，则c=3 其中结论正确的是 （ ）

    A. （1）（2） B. （2）（3） C. （3）（4） D. （1）（4）

    【答案】B

    【解析】解：（1）令x=0，得：y1=（0-2）2+1=5，∴抛物线y1与y轴的交点坐标为（0，5），故（1）错误；

    （2）当x=－4时，y1=（－4－2）2+1=37，∴m=37，当x=7时，y1=（7－2）2+1=26，∴n=26，∴m＞n，故（2）正确；

    （3）当x=1时，y2=12-4+c=－3+c．∵点B在点A的上方，∴－3+c＞－3，解得：c＞0．故（3）正确；

    （4）令x=1，得：y1=（1-2）2+1=2，∴BC=|－3+c -2|=2，解得：c=3或c=7．故（4）错误．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我们规定：若关于x的一元一次方程ax＝b的解为b+a，则称该方程为“和解方程”． 例如：方程2x＝﹣4的解为x＝﹣2，而﹣2＝﹣4+2，则方程2x＝﹣4为“和解方程”．

    请根据上述规定解答下列问题：

    （1）已知关于x的一元一次方程3x＝m是“和解方程”，求m的值；

    （2）已知关于x的一元一次方程﹣2x＝mn+n是“和解方程”，并且它的解是x＝n，求m，n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

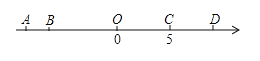
    【题目】如图，数轴上有A、B、C、D、O五个点，点O为原点，点C在数轴上表示的数是5，线段CD的长度为4个单位，线段AB的长度为2个单位，且B、C两点之间的距离为11个单位，请解答下列问题：

    （1）点D在数轴上表示的数是 ，点A在数轴上表示的数是 ；

    （2）若点B以每秒2个单位的速度向右匀速运动t秒运动到线段CD上，且BC的长度是3个单位，根据题意列出的方程是 ，解得t= ；

    （3）若线段AB、CD同时从原来的位置出发，线段AB以每秒2个单位的速度向右匀速运动，线段CD以每秒3个单位的速度向左匀速运动，把线段CD的中点记作P，请直接写出，点P与线段AB的一个端点的距离为1.5个单位时运动的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有长为30m的篱笆，一面利用墙（墙的最大可用长度为10m），围成中间隔有一道篱笆（平行于AB）的矩形花圃．设花圃的一边AB为xm，面积为ym2．

    （1）求y与x的函数关系式；

    （2）如果要围成面积为63m2的花圃，AB的长是多少？

    （3）能围成比63m2更大的花圃吗？如果能，请求出最大面积；如果不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】目前，我市城市居民用电收费方式有以下两种:

    普通电价付费方式:全天0. 52元/度;

    峰谷电价付费方式:峰时(早8:00~晚21:00)0. 65元/度;谷时(晚21:00~早8:00)0. 40元/度.

    (1)小丽老师家10月份总用电量为280度.

    ①若其中峰时电量为80度，则小丽老师家按照哪种方式付电费比较合适?能省多少元?

    ②若小丽老师交费137元，那么，小丽老师家峰时电量为多少度?

    (2)到11月份付费时，小丽老师发现11月份总用电量为320度，用峰谷电价付费方式比普通电价付费方式省了18. 4元，那么，11月份小丽老师家峰时电量为多少度?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读以下证明过程：

    已知：在△ABC中，∠C≠90°，设AB=c，AC=b，BC=a．求证：a2+b2≠c2．

    证明：假设a2+b2=c2，则由勾股定理逆定理可知∠C=90°，这与已知中的∠C≠90°矛盾，故假设不成立，所以a2+b2≠c2．

    请用类似的方法证明以下问题：

    已知：关于x的一元二次方程x2﹣（m+1）x+2m-3=0 有两个实根x1和x2．

    求证：x1≠x2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形ABCD中，点C（3，8），E、F为AB、CD边上的中点，如图1，点A在原点处，点B在y轴正半轴上，点C在第一象限，若点A从原点出发，沿x轴向右以每秒1个单位长度的速度运动，点B随之沿y轴下滑，并带动矩形ABCD在平面内滑动，如图2，设运动时间表示为t秒，当点B到达原点时停止运动．

    （1）当t=0时，点F的坐标为 ；

    （2）当t=4时，求OE的长及点B下滑的距离；

    （3）求运动过程中，点F到点O的最大距离；

    （4）当以点F为圆心，FA为半径的圆与坐标轴相切时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】因课外阅读需要，学校图书馆向出版商邮购某系列图书，每本书单价为20元，邮购总费用包括书的价钱和邮费．相关的书价折扣、邮费如下表所示．

    数量

    折扣

    邮费（元/次）

    不超过10本

    九折

    6元

    超过10本

    八折

    实际总书价的10%

    （1）若一次邮购8本，共需总费用为 元.

    若一次邮购12本，共需总费用为 元.

    （2）已知图书馆需购书的总数是10的整数倍，且超过10本．

    ①若分次邮购、分别汇款，每次邮购10本，总费用为930元时，共邮购了多少本书？

    ②如果图书馆需购书的总数为60本，若你是图书馆负责人，从节约的角度出发，在 “每次邮购10本”与“一次性邮购”这两种方式中你会选择哪一种？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，Rt△ABC中，∠B=90°，∠CAB=30°，它的顶点A的坐标为（10，0），顶点B的坐标为（5，5），AB=10，点P从点A出发，沿A→B→C的方向匀速运动，同时点Q从点D（0，2）出发，沿y轴正方向以相同速度运动，当点P到达点C时，两点同时停止运动，设运动的时间为t秒．

    （1）当点P在AB上运动时，△OPQ的面积S（平方单位）与时间t（秒）之间的函数图象为抛物线的一部分，（如图②），则点P的运动速度为 ；

    （2）求（1）中面积S与时间t之间的函数关系式及面积S的最大值及S取最大值时点P的坐标；

    （3）如果点P，Q保持（1）中的速度不变，那么点P沿AB边运动时，∠OPQ的大小随着时间t的增大而增大；沿着BC边运动时，∠OPQ的大小随着时间t的增大而减小，当点P沿这两边运动时，使∠OPQ=90°的点P有 个．

    查看答案和解析>>

    同步练习册答案