
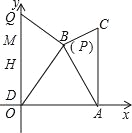
【题目】如图①,Rt△ABC中,∠B=90°,∠CAB=30°,它的顶点A的坐标为(10,0),顶点B的坐标为(5,5![]() ),AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
),AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
(1)当点P在AB上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分,(如图②),则点P的运动速度为 ;
(2)求(1)中面积S与时间t之间的函数关系式及面积S的最大值及S取最大值时点P的坐标;
(3)如果点P,Q保持(1)中的速度不变,那么点P沿AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小,当点P沿这两边运动时,使∠OPQ=90°的点P有 个.

【答案】(1)2个单位/秒;(2)S=![]() (2t+2)(10﹣t),当t=
(2t+2)(10﹣t),当t=![]() 时,S有最大值为
时,S有最大值为![]() ,此时P(
,此时P(![]() );(3)2.
);(3)2.
【解析】试题分析:(1)由图形可知,当点P运动了5秒时,它到达点B,此时![]() 即可求出点P的运动速度.
即可求出点P的运动速度.
![]() 过P作
过P作![]() 轴,表示出
轴,表示出![]()
![]()
![]() 配方求出最大值即可.
配方求出最大值即可.
![]() 分两种情况进行讨论即可.
分两种情况进行讨论即可.
试题解析:(1)由图形可知,当点P运动了5秒时,它到达点B,此时![]() 因此点P的运动速度为10÷5=2个单位/秒,
因此点P的运动速度为10÷5=2个单位/秒,
点P的运动速度为2个单位/秒.
故答案是:2个单位/秒;
(2)如图①,过P作![]() 轴,
轴,
∵点P的运动速度为2个单位/秒.
∴t秒钟走的路程为2t,即![]()
∵顶点B的坐标为![]()
∴![]()
∴![]()
∴![]()
∴![]() 又
又![]()
∴![]() 即为
即为![]() 中OQ边上的高,
中OQ边上的高,
而![]() 可得
可得![]()
∴![]()
∵![]()
![]()
∴当![]() 时,S有最大值为
时,S有最大值为![]() ,此时P
,此时P .
.
(3)当点P沿这两边运动时, ![]() 的点P有2个.
的点P有2个.
①当点P与点A重合时, ![]()
当点P运动到与点B重合时,OQ的长是12单位长度,
作![]() 交y轴于点M,作
交y轴于点M,作![]() 轴于点H,
轴于点H,
由![]() 得:
得: ![]()
所以![]() ,从而
,从而![]()
所以当点P在AB边上运动时, ![]() 的点P有1个.
的点P有1个.
②同理当点P在BC边上运动时,可算得, ![]()
而构成直角时交y轴于
所以![]() 从而
从而![]() 的点P也有1个.
的点P也有1个.
所以当点P沿这两边运动时, ![]() 的点P有2个.
的点P有2个.
故答案是:2.



 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y1=(x-2)2+1与y2=x2-4x+c,过点A(1,-3)作直线l∥y轴,交抛物线y2于点B,交抛物线y1于 点C,则以下结论:
(1)抛物线y1与y轴的交点坐标为(0,1)
(2)若点D(-4,m)及点E(7,n)均在抛物线y1上,则m>n;
(3)若点B在点A的上方,则c>0;(4)若BC=2,则c=3 其中结论正确的是 ( )

A. (1)(2) B. (2)(3) C. (3)(4) D. (1)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
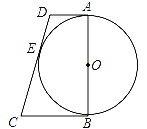
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一张边长为![]() 的正方形纸片
的正方形纸片![]() ,点
,点![]() 为正方形
为正方形![]() 边上的一点(不与点
边上的一点(不与点![]() ,点
,点![]() 重合)将正方形纸片折叠,使点
重合)将正方形纸片折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,点
处,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于
于![]() ,折痕为
,折痕为![]() ,连接
,连接![]() ,
,![]() .则
.则![]() 的周长是______.
的周长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx﹣2与x轴交于点A(﹣1,0),B(4,0)两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).
(1)求该抛物线的解析式;
(2)如图2,过点A作BE的平行线交抛物线于另一点D,点P是抛物线上位于线段AD下方的一个动点,连结PA,EA,ED,PD,求四边形EAPD面积的最大值;
(3)如图3,连结AC,将△AOC绕点O逆时针方向旋转,记旋转中的三角形为△A′OC′,在旋转过程中,直线OC′与直线BE交于点Q,若△BOQ为等腰三角形,请直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是正方形
是正方形![]() 的对角线
的对角线![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() .给出下列五个结论:①
.给出下列五个结论:①![]() ;②
;②![]() 一定是等腰直角三角形;③
一定是等腰直角三角形;③![]() 一定是等腰三角形;④
一定是等腰三角形;④![]() ;⑤
;⑤![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A. ①②③④B. ①②④⑤C. ②③④⑤D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
甲、乙两人同时从相距25千米的A地去B 地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=![]() 相交于点A(m,6)和点B(﹣3,n),直线AB与y轴交于点C.
相交于点A(m,6)和点B(﹣3,n),直线AB与y轴交于点C.
(1)求直线AB的表达式;
(2)求AC:CB的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com