
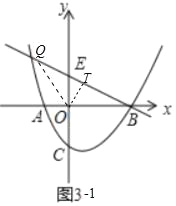
����Ŀ����ͼ1��������y=ax2+bx��2��x�ύ�ڵ�A����1��0����B��4��0�����㣬��y�ύ�ڵ�C��������B��ֱ�߽�y���ڵ�E��0��2����
��1����������ߵĽ���ʽ��
��2����ͼ2������A��BE��ƽ���߽�����������һ��D����P����������λ���߶�AD�·���һ�����㣬����PA��EA��ED��PD�����ı���EAPD��������ֵ��
��3����ͼ3������AC������AOC�Ƶ�O��ʱ�뷽����ת������ת�е�������Ϊ��A��OC��������ת�����У�ֱ��OC����ֱ��BE���ڵ�Q������BOQΪ���������Σ���ֱ��д����Q�����꣮

���𰸡���1��y=![]() x2��
x2��![]() x��2����2��9����3��Q��������
x��2����2��9����3��Q��������![]() ����4��
����4��![]() ����2��1����4+
����2��1����4+![]() ����
����![]() ����
����
����������������� ![]() �ѵ�
�ѵ�![]() ����������
����������![]() �����
�����![]() ��ֵ����.
��ֵ����.
![]() ���ô���ϵ�������ֱ��BE�Ľ���ʽ���������ֱ��AD�Ľ���ʽ����
���ô���ϵ�������ֱ��BE�Ľ���ʽ���������ֱ��AD�Ľ���ʽ����![]() ��
��![]() ��ʾ��
��ʾ��![]() ,���䷽������������ֵ��
,���䷽������������ֵ��
�������� �����
�����![]() �����꣬
�����꣬ ![]() ���ֵ=
���ֵ=![]() ��
��
���������ı���EAPD��������ֵ��
![]() ����������������ۼ���.
����������������ۼ���.
�����������1����![]() ��������
��������![]() �ϣ�
�ϣ�
��![]()
���
�������ߵĽ���ʽΪ![]()
��2������P��![]() �ύAD�ڵ�G��
�ύAD�ڵ�G��

��![]()
��ֱ��BE�Ľ���ʽΪ![]()
��AD��BE����ֱ��AD�Ľ���ʽΪ![]() ����
����![]() ���ɵ�
���ɵ�![]()
��ֱ��AD�Ľ���ʽΪ![]()
��![]() ��
��![]()
��![]()
�൱x=1ʱ��PG��ֵ������ֵΪ2��
�� ���
���![]() ��
��![]()
��![]()
��![]() ���ֵ=
���ֵ=![]()
![]()
��AD��BE��
��![]()
��S�ı���APDE���=S��ADP���+![]()
��3������ͼ3��1�У���![]() ʱ����
ʱ����![]() ��T��
��T��
��![]()
��![]()
��![]()
��![]()
�ɵ�![]()
����ͼ3��2�У���![]() ʱ,
ʱ, 
��![]() ʱ��
ʱ�� ![]()
��![]() ʱ��Q3
ʱ��Q3
���������������������Q����Ϊ![]() ��
�� ��
��![]() ��
��


 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����֤�����̣�
��֪���ڡ�ABC�У���C��90�㣬��AB=c��AC=b��BC=a����֤��a2+b2��c2��
֤��������a2+b2=c2�����ɹ��ɶ����涨����֪��C=90�㣬������֪�еġ�C��90��ì�ܣ��ʼ��費����������a2+b2��c2��
�������Ƶķ���֤���������⣺
��֪������x��һԪ���η���x2����m+1��x+2m-3=0 ������ʵ��x1��x2��
��֤��x1��x2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ����װ���������װÿ����500Ԫ�����ÿ������100Ԫ��Ԫ���ס������̼Ҵ�������
���̳�����һ����װ��һ�������
���̳�����װ������������۵�![]() ���
���
��ij�ͻ�Ҫ������װ10�ף����![]() ��
��![]() ��
��
��1�����ÿͻ�ȥ���̳������踶�����Ԫ�����ú�![]() �Ĵ���ʽ��ʾ�����ÿͻ�ȥ���̳������踶�����Ԫ�����ú�
�Ĵ���ʽ��ʾ�����ÿͻ�ȥ���̳������踶�����Ԫ�����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2����![]() ����20��ͨ������˵����ʱȥ�ļ��̳�������㣿
����20��ͨ������˵����ʱȥ�ļ��̳�������㣿
��3����![]() ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�����
ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A(��4��n)��B(2����4)��һ�κ���y��kx��b�ͷ���������y��![]() ��ͼ����������㣮
��ͼ����������㣮

(1)��һ�κ����ͷ����������Ľ���ʽ��
(2)���AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90������CAB=30�������Ķ���A������Ϊ��10��0��������B������Ϊ��5��5![]() ����AB=10����P�ӵ�A��������A��B��C�ķ��������˶���ͬʱ��Q�ӵ�D��0��2����������y������������ͬ�ٶ��˶�������P�����Cʱ������ͬʱֹͣ�˶������˶���ʱ��Ϊt�룮
����AB=10����P�ӵ�A��������A��B��C�ķ��������˶���ͬʱ��Q�ӵ�D��0��2����������y������������ͬ�ٶ��˶�������P�����Cʱ������ͬʱֹͣ�˶������˶���ʱ��Ϊt�룮
��1������P��AB���˶�ʱ����OPQ�����S��ƽ����λ����ʱ��t���룩֮��ĺ���ͼ��Ϊ�����ߵ�һ���֣�����ͼ���������P���˶��ٶ�Ϊ ��
��2����1�������S��ʱ��t֮��ĺ�����ϵʽ�����S�����ֵ��Sȡ���ֵʱ��P�����ꣻ
��3�������P��Q���֣�1���е��ٶȲ��䣬��ô��P��AB���˶�ʱ����OPQ�Ĵ�С����ʱ��t���������������BC���˶�ʱ����OPQ�Ĵ�С����ʱ��t���������С������P���������˶�ʱ��ʹ��OPQ=90���ĵ�P�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ����������ϵ�ԭ�㿪ʼ���������ƶ�3����λ���ȣ��������ƶ�5����λ���ȣ����Կ����յ��ʾ�����ǩ�2����֪��A��B�������ϵĵ㣬�����ͼ��˼����������и��⣮

��1�������A��ʾ����3������A�����ƶ�7����λ���ȣ���ô�յ�B��ʾ�������� ����A��B�����ľ������� ����
��2�������A��ʾ��3����A�������ƶ�7����λ���ȣ��������ƶ�5����λ���ȣ���ô�յ�B��ʾ�������� ����A��B�����ľ���Ϊ�� ����
��3�������A��ʾ����4����A�������ƶ�16����λ���ȣ��������ƶ�25����λ���ȣ���ô�յ�B��ʾ�������� ����A��B�����ľ������� ����
��4��һ��أ����A���ʾ����Ϊm����A�������ƶ�n����λ���ȣ��������ƶ�p����λ���ȣ���ô��������յ�B��ʾʲô����A��B�����ľ���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ֽƬABCD�����Խ���AC��BD���ڵ�O���۵�������ֽƬABCD��ʹAD����BD������Aǡ����BD�ϵĵ�F�غϣ�չ�������ۺ�DE�ֱ�AB��AC�ڵ�E��G������GF�����н������١�AGD=112.5������tan��AED=2����S��AGD=S��OGD�����ı���AEFG����������BE=2OG��
������ȷ���۵��������������

A. �٢ڢۢܢ� B. �٢ڢۢ� C. �٢ۢܢ� D. �٢ܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊʵʩ�������ս�ԣ����ijɽ���ϰ��ճ����ѵ����⣬��������������һ�����ٹ�·.����һ�γ�Ϊ146��ɽ�������ᴩ�����ɼ����������̶Ӹ���ʩ��.���̶Ӷ�������2����ҹ��̶Ӽ��룬�����̶������Ϲ�����1�죬��3�칲���26��.��֪���̶�ÿ����ҹ��̶Ӷ���2�ף������ٶ�������������ᴩ���̣������������̶ӻ������Ϲ��������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���ܵ��ڳ����ѻ����ռ���ij�̳��ƻ������ס������ֽ��ܵƹ�1200ֻ�������ֽ��ܵƵĽ��ۡ��ۼ����±���
| ���� | �ۼ� |
���� | 25 | 30 |
���� | 45 | 60 |
![]() ��ν�����������ǡ��Ϊ46000Ԫ��
��ν�����������ǡ��Ϊ46000Ԫ��
![]() Ϊȷ�����ͽ��ܵ�˳����������
Ϊȷ�����ͽ��ܵ�˳����������![]() �������£��̼Ҿ��������ͽ��ܵƽ��д��۳��ۣ���ȫ����������ͽ��ܵƵ�������Ϊ
�������£��̼Ҿ��������ͽ��ܵƽ��д��۳��ۣ���ȫ����������ͽ��ܵƵ�������Ϊ![]() ���������ͽ��ܵ�����ۣ�
���������ͽ��ܵ�����ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com