
【题目】如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.

(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
【答案】(1)y=-![]() , y=-x-2;(2)6.
, y=-x-2;(2)6.
【解析】
(1)将B代入反比例函数中,求出m的值,再求出A的坐标,分别将A、B的坐标代入一次函数图象,求出一次函数的解析式,
(2)设一次函数y=-x-2的图象与y轴交于C点,求出C点坐标,得到OC的长度,再求出S△ACO,S△BCO两个相加后,S△AOB=S△ACO+S△BCO得到答案.
(1)∵B(2,-4)在y=![]() 图象上,∴m=-8.
图象上,∴m=-8.
∴反比例函数的解析式为y=-.
∵点A(-4,n)在y=-图象上,∴n=2,∴A(-4,2).
∵一次函数y=kx+b图象经过A(-4,2),B(2,-4),
∴![]() ,解得
,解得![]() .
.
∴一次函数的解析式为y=-x-2.
(2)设一次函数y=-x-2的图象与y轴交于C点,
当x=0时,y=-2,∴点C(0,-2).
∴OC=2,
∴S△AOB=S△ACO+S△BCO=×2×4+×2×2=6.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】在《丰富的图形世界》一章中,我们认识了三棱柱、四棱柱、五棱柱和六棱柱,这些棱柱是由点、线和面构成.
(1)请使用合适的方式统计上述四种棱柱顶点的个数、棱的条数和面的个数;
(2)若棱柱顶点的个数用V表示、棱的条数用E表示、面的个数用F表示,观察你的统计数据,写出V,E,F三者间的数量关系;
(3)若某几何体满足(2)的数量关系,且有24条棱和10个面,则几何体有多少个顶点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法综宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,则小和尚有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB、a、b.
(1)请用尺规按下列要求作图:(不要求写作法,但要保留作图痕迹)
①延长线段AB到C,使BC=a;
②反向延长线段AB到D,使AD=b.
(2)在(1)的条件下,如果AB=8cm,a=6m,b=10cm,且点E为CD的中点,求线段AE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
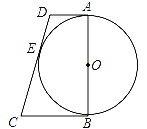
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装网店批发商批发一种童装,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.经调查,如果每件童装降价
元.经调查,如果每件童装降价![]() 元,那么平均每天就可多售出
元,那么平均每天就可多售出![]() 件.
件.
(1)设每件童装降价![]() 元,那么每天可售出多少件童装?每件童装的利润是多少元?(用含
元,那么每天可售出多少件童装?每件童装的利润是多少元?(用含![]() 的代数式表示)
的代数式表示)
(2)为了迎接“六一”儿童节,商家决定降价促销、尽快减少库存,又想保证平均每天盈利![]() 元,求每件童装应降价多少元?
元,求每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx﹣2与x轴交于点A(﹣1,0),B(4,0)两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).
(1)求该抛物线的解析式;
(2)如图2,过点A作BE的平行线交抛物线于另一点D,点P是抛物线上位于线段AD下方的一个动点,连结PA,EA,ED,PD,求四边形EAPD面积的最大值;
(3)如图3,连结AC,将△AOC绕点O逆时针方向旋转,记旋转中的三角形为△A′OC′,在旋转过程中,直线OC′与直线BE交于点Q,若△BOQ为等腰三角形,请直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
(1)用代数式表示这两个篮球场的占地面积.
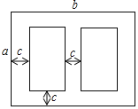
(2)当a=30,b=40,c=3时,计算出一个篮球场的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
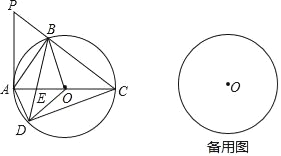
【题目】如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.
(1)求证:AP为⊙O的切线;
(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com