
【题目】商场某种商品平均每天可销售40件,每件盈利50元,为了减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.
(1)若某天该商品每件降价a元,当天可卖多少件?
(2)在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到2400元?
(3)每件商品降价多少元时,商场日盈利最大?
【答案】(1)![]() 件;(2)10元或20元;(3)每件商品降价15元时,商场日盈利最大.
件;(2)10元或20元;(3)每件商品降价15元时,商场日盈利最大.
【解析】
(1)根据降价1元,可多售出2件,得出降价a元,可多售出2a件,销售的件数=原来销售的件数+多销售的件数;
(2)根据每件商品的盈利×可卖出商品的件数=2400,列出方程进行求解即可.
(3)根据利润=每件商品的盈利![]() 卖出商品的件数,化成一般式后,配方可得结论.
卖出商品的件数,化成一般式后,配方可得结论.
解:(1)![]() 件
件
(2)设每件商品降价![]() 元。由题意得:
元。由题意得:
![]() .即
.即![]()
解这个方程,得![]() ,
,![]()
答:每件商品降价10元或20元时,商场日盈利可达到2400元.
(3)设每件商品降价![]() 元,商场日盈利为
元,商场日盈利为![]() 元,由题意得:
元,由题意得:![]()
![]()
![]() .
.![]()
所以,当![]() 时,
时,![]() 的值最大.
的值最大.
故:每件商品降价15元时,商场日盈利最大.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】设双曲线y=![]() (k>0)与直线y=x交于A\B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P、Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径“,当双曲线y=
(k>0)与直线y=x交于A\B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P、Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径“,当双曲线y=![]() (k>0)的眸径为6时,k的值为( )
(k>0)的眸径为6时,k的值为( )
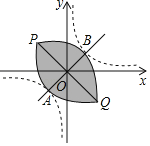
A.![]() B.2C.
B.2C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
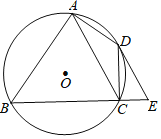
【题目】如图,四边形ABCD内接于⊙O,∠DAB=90°,点E在BC的延长线上,且∠CED=∠CAB.
(1)求证:DE是⊙O的切线.
(2)若AC∥DE,当AB=8,DC=4时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长![]() 、宽
、宽![]() 的矩形纸板。将纸板四个角各剪去一个边长为
的矩形纸板。将纸板四个角各剪去一个边长为![]() 的正方形,然后将四周突出部分折起,可制成一个底面积是
的正方形,然后将四周突出部分折起,可制成一个底面积是![]() 的无激长方体纸盒,则
的无激长方体纸盒,则![]() 的值为__________.
的值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数 | 30 | 75 | 130 | 210 | 480 | 856 | 1250 | 2300 |
发芽数 | 28 | 72 | 125 | 200 | 457 | 814 | 1187 | 2185 |
发芽频率 | 0.9333 | 0.9600 | 0.9615 | 0.9524 | 0.9521 | 0.9509 | 0.9496 | 0.9500 |
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是_____(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )

A. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
B. 掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C. 在“石头剪刀、和”的游戏中,小明随机出的是“剪刀”
D. 袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲车从![]() 地出发匀速驶向
地出发匀速驶向![]() 地,到达
地,到达![]() 地后,立即按原路原速返回
地后,立即按原路原速返回![]() 地;乙车从
地;乙车从![]() 地出发沿相同的路线匀速驶向
地出发沿相同的路线匀速驶向![]() 地,出发
地,出发![]() 小时后,乙车因故障在途中停车
小时后,乙车因故障在途中停车![]() 小时,然后继续按原速驶向
小时,然后继续按原速驶向![]() 地,乙车在行驶过程中的速度是
地,乙车在行驶过程中的速度是![]() 千米/时,甲车比乙车早
千米/时,甲车比乙车早![]() 小时到达
小时到达![]() 地,两车距各自出发地的路程
地,两车距各自出发地的路程![]() 千米与甲车行驶时间
千米与甲车行驶时间![]() 小时之间的函数关系式如图所示,请结合图象信息解答下列问题:
小时之间的函数关系式如图所示,请结合图象信息解答下列问题:

(1)写出甲车行驶的速度,并直接写出图中括号内正确的数 ;
(2)求甲车从![]() 地返回
地返回![]() 地的过程中,
地的过程中,![]() 与
与![]() 的函数关系式(不需要写出自变量x的取值范围)
的函数关系式(不需要写出自变量x的取值范围)
(3)直接写出乙车出发多少小时,两车恰好相距![]() 千米.
千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com