【题目】如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．
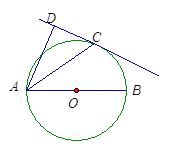
（1）求证：AD⊥DC；
（2）若AD＝2，AC＝
，求AB的长．
【答案】（1）略 （2）2.5
【解析】
（1）连接OC，根据切线的性质得到OC与CD垂直，进而得到∠OCA+∠DCA=90°，由AC为角平分线，根据角平分线定义得到两个角相等，又OA=OC，根据等边对等角得到又得到另两个角相等，等量代换后得到∠DAC=∠OCA，根据等角的余角相等得到∠DCA+∠DAC=90°，从而得到∠ADC为直角，得证；
（2）连接CB，由AB为圆O的直径，根据直径所对的圆周角为直角得到∠ACB与∠ADC相等都为直角，又根据AC为角平分线得到一对角相等，由两对对应角相等的两三角形相似，得到三角形ADC与三角形ABC相似，由相似得比例列出关系式，把AC和AD的长即可求出AB的长．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】二次函数y=ax2＋bx＋c(a≠0)的图象如图所示，根据图象解答下列问题．
(1)写出方程ax2＋bx＋c＝0的两个根；
(2)写出不等式ax2＋bx＋c＞0的解集；
(3)写出y随x的增大而减小的自变量x的取值范围；
(4)若方程ax2＋bx＋c＝k有两个不相等的实数根，求k的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】商场某种商品平均每天可销售40件，每件盈利50元，为了减少库存，商场决定采取适当的降价措施.经调查发现，每件商品每降价1元，商场平均每天可多售出2件.
（1）若某天该商品每件降价a元，当天可卖多少件？
（2）在上述销售正常情况下，每件商品降价多少元时，商场日盈利可达到2400元？
（3）每件商品降价多少元时，商场日盈利最大？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y=kx+5(k为常数，且k≠0)的图像与反比例函数y=-
的函数交于A、B(4，b)两点.
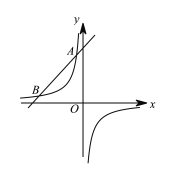
(1)求一次函数的表达式及A点的坐标；
(2)直接写出一次函数的值大于反比例函数的值时，自变量x的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
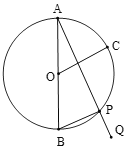
【题目】如图，AB为⊙O的直径，AB＝3，弧AC的度数是
，P为弧BC上一动点，延长AP到点Q，使
.若点P由B运动到C，则点Q运动的路径长为______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在⊙O中，弦BC垂直于半径OA，垂足为E，D是优弧BC上一点，连结BD，AD，OC，∠ADB＝30°.
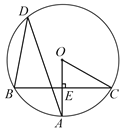
(1)求∠AOC的度数；
(2)若弦BC＝6 cm，求图中劣弧BC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y= ax2+bx+c(a≠0)对称轴为直线x=1，与x轴的一个交点坐标为(-1，0)，与y轴交点为(0，3)，其部分图象如图所示，则下列结论错误的是( )
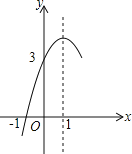
A.a-b+c=0B.关于x的方程ax2+bx+c- 3=0有两个不相等的实数根
C.abc>0D.当y>0时，-1<x<3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，点E为BC的中点，AE与对角线BD交于点F.
（1）求证：DF=2BF；
（2）当∠AFB=90°且tan∠ABD=
时， 若CD=
，求AD长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
