
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.

(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
【答案】(1)x=1或x=3是方程ax2+bx+c=0的两个根;(2)l<x<3;(3)当x>2时,y随x的增大而减小;(4)k<2.
【解析】试题分析:(1)观察图形可以看出抛物线与x轴交于(1,0)和(3,0),即可解题
(2)根据抛物线y=ax2+bx+c,求得y>0的x取值范围即可解题;
(3)图中可以看出抛物线对称轴,即可解题;
(3)易求得抛物线解析式,根据方程△>0即可解题.
试题解析:(1)图中可以看出抛物线与x轴交于(1,0)和(3,0),
∴方程ax2+bx+c=0的两个根为x=1或x=3;
(2)不等式ax2+bx+c>0时,通过图中可以看出:当1<x<3时,y的值>0,
∴不等式ax2+bx+c>0的解集为(1,3);
(3)图中可以看出对称轴为x=2,
∴当x>2时,y随x的增大而减小;
(4)∵抛物线y=ax2+bx+c经过(1,0),(2,2),(3,0),
∴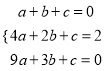 ,
,
解得:a=2,b=8,c=6,
∴2x2+8x6=k,移项得2x2+8x6k=0,
△=644(2)(6k)>0,
整理得:168k>0,
∴k<2时,方程ax2+bx+c=k有2个相等的实数根。


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:![]() ;
;![]() 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若![]() >0,
>0,![]() >0,则
>0,则![]() >0;若
>0;若![]() <0,
<0,![]() <0,则
<0,则![]() >0;
>0;
(2)若![]() >0,
>0,![]() <0,则
<0,则![]() <0;若
<0;若![]() <0,
<0,![]() >0,则
>0,则![]() <0.
<0.
反之:(1)若![]() >0,则
>0,则![]() 或
或![]()
(2)若![]() <0,则__________或__________.
<0,则__________或__________.
(3)根据上述规律,求不等式![]() 的解集.
的解集.
(4)试求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连结CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
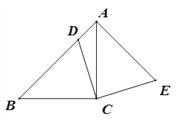
(1)求证:AB⊥AE;
(2)若![]() ,求证:四边形ADCE为正方形.
,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
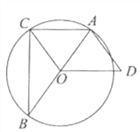
【题目】如图,已知△ABC内接于![]() ,AB是直径,OD∥AC,AD=OC.
,AB是直径,OD∥AC,AD=OC.
(1)求证:四边形OCAD是平行四边形;
(2)填空:①当∠B= 时,四边形OCAD是菱形;
②当∠B= 时,AD与![]() 相切.
相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正方体的六个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问:长方体的下底面共有多少朵花?
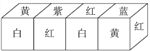
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
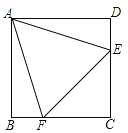
【题目】正方形ABCD中,点E、F分别在CD、BC边上,![]() 是等边三角形.以下结论:①
是等边三角形.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④EF的垂直平分线是直线AC.正确结论个数有( )个.
;④EF的垂直平分线是直线AC.正确结论个数有( )个.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面方格中有一个四边形ABCD和点O,请在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).
(1)画出四边形ABCD以点O为旋转中心,逆时针旋转90°后得到的四边形A1B1C1D1;
(2)画出四边形A1B1C1D1向右平移3格(3个小方格的边长)后得到的四边形A2B2C2D2;
(3)填空:若每个小方格的边长为1,则四边形A1B1C1D1与四边形A2B2C2D2重叠部分的面积为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com