
【题目】正方形ABCD中,点E、F分别在CD、BC边上,![]() 是等边三角形.以下结论:①
是等边三角形.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④EF的垂直平分线是直线AC.正确结论个数有( )个.
;④EF的垂直平分线是直线AC.正确结论个数有( )个.
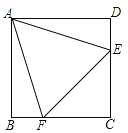
A.1B.2C.3D.4
【答案】C
【解析】
由题意可证△ABF≌△ADE,可得BF=DE,即可得EC=CF,由勾股定理可得EF=![]() EC,由平角定义可求∠AED=75°,由AE=AF,EC=FC可证AC垂直平分EF,则可判断各命题是否正确.
EC,由平角定义可求∠AED=75°,由AE=AF,EC=FC可证AC垂直平分EF,则可判断各命题是否正确.
解:∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠C=∠D=∠DAB=90°,
∵△AEF是等边三角形,
∴AE=AF=EF,∠EAF=∠AEF=60°,
∵AD=AB,AF=AE,
∴△ABF≌△ADE,
∴BF=DE,
∴BCBF=CDDE,
∴CE=CF,故①正确;
∵CE=CF,∠C=90°;
∴EF=![]() CE,∠CEF=45°;
CE,∠CEF=45°;
∴AF=![]() CE,
CE,
∴CF=![]() AF,故③错误;
AF,故③错误;
∵∠AED=180°∠CEF∠AEF;
∴∠AED=75°;故②正确;
∵AE=AF,CE=CF;
∴AC垂直平分EF;故④正确.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,点0为直线AB上一点,∠AOC=50![]() ,OD平分∠AOC,∠DOE=90
,OD平分∠AOC,∠DOE=90![]() .
.
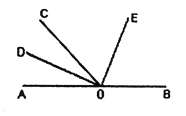
(1)请你数一数,图中有多少个小于平角的角:
(2)求出∠BOD的度数;
(3)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.

(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
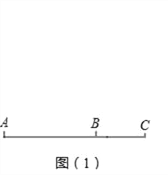
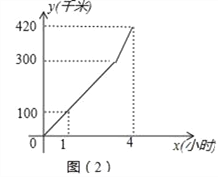
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一货轮在C处测得灯塔A在货轮的北偏西30的方向上,随后货轮以80海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB(结果保留3个有效数字, ![]() ≈2.449).
≈2.449).
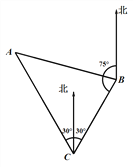
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个由正奇数排成的数阵.用如图所示的四边形框去框住四个数.

(1)若设框住四个数中左上角的数为n,则这四个数的和为 (用n的代数式表示);
(2)平行移动四边形框,若框住四个数的和为228,求出这4个数;
(3)平行移动四边形框,能否使框住四个数的和为508?若能,求出这4个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点.
(1)若点A(0.5,0)和点B(1.5,0),求抛物线的表达式;
(2)三角形的内心是________的交点.在(1)的条件下,抛物线与y轴交于点C,点D在x轴上,且坐标为(-3,0),直线l经过点C、D.在抛物线上是否存在一点P,使△DCP的内心在y轴上,若存在,求出点P的坐标,若不存在,请说明理由;
(3)是否存在整数a,b,使得1<x1<2和1<x2<2同时成立?证明你的结论.
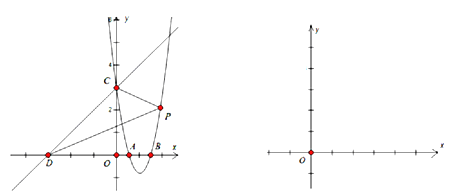
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
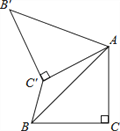
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动
问题情境:
如图1,在ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将ADE绕点A顺时针旋转α角(0°<α<90°)得到AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
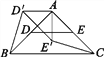 图1
图1 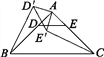 图2
图2 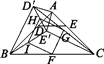 图3
图3 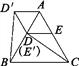 图4
图4
探究发现:
(1)图1中,CE′与BD′的数量关系是________;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E”,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
(3)如图3,在(2)的条件下,连接BE′,CD′,分别取BC,CD′,E′D′,BE′的中点F,G,H,I,顺次连接F,G,H,I得到四边形FGHI.请判断四边形FGHI的形状,并说明理由;
(4)如图4,在ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将ADE绕点A顺时针旋转60°得到AD′E′,连接CE′,BD′.请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com