
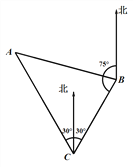
【题目】一货轮在C处测得灯塔A在货轮的北偏西30的方向上,随后货轮以80海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB(结果保留3个有效数字, ![]() ≈2.449).
≈2.449).
【答案】49.0
【解析】试题分析:过B作BD⊥AC于D.可先由速度和时间求出BC的距离,再由各方向角得出∠A的度数,进而求出∠DBC的度数,求出DC,由勾股定理求出BD,求出AD、BD的长,由勾股定理求出AB即可.
试题解析:解:过B作BD⊥AC于D.由示意图可知:∠ACB=60°,由平行线的性质可知∠ABC=180°﹣30°﹣75°=75°,∴∠A=180°﹣∠C﹣∠B=45°,BC=80×![]() =40(海里).∵∠BDC=90°,∠ACB=60°,∴∠DBC=30°,∴DC=
=40(海里).∵∠BDC=90°,∠ACB=60°,∴∠DBC=30°,∴DC=![]() BC=20海里, BD=
BC=20海里, BD=![]() 海里.∵∠A=45°,∠ADB=90°,∴∠ABD=∠A=45°,∴AD=BD=
海里.∵∠A=45°,∠ADB=90°,∴∠ABD=∠A=45°,∴AD=BD=![]() 海里,由勾股定理得:AB=
海里,由勾股定理得:AB=![]() =
=![]() ≈49.0(海里).
≈49.0(海里).
答:此时货轮距灯塔A的距离AB为49.0海里.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+2与反比例函数y2=![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
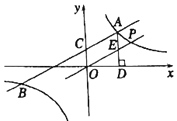
(1)k1= ,k2= ;
(2)根据函数图象可知,当y1>y2时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求直线OP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种学生用计算器,进价为每台20元,售价为每台30元时,每周可卖160台,如果每台售价每上涨2元,每周就会少卖20台,但厂家规定最高每台售价不能超过33元,当计算器定价为多少元时,商场每周的利润恰好为1680元?
查看答案和解析>>
科目:初中数学 来源: 题型:
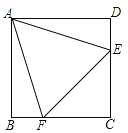
【题目】正方形ABCD中,点E、F分别在CD、BC边上,![]() 是等边三角形.以下结论:①
是等边三角形.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④EF的垂直平分线是直线AC.正确结论个数有( )个.
;④EF的垂直平分线是直线AC.正确结论个数有( )个.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位数,百位数是![]() ,十位数是
,十位数是![]() ,个位数是
,个位数是![]() ,我们可以记作
,我们可以记作![]() ,
, ![]() 表示,例如
表示,例如![]() ,仿照上面的例子,
,仿照上面的例子,
(1)![]() 可以用 表示;
可以用 表示;
(2)![]() 可以用 表示;
可以用 表示;
(3)欧阳老师给4为同学玩一个数字游戏,先请A同学心里想一个三位数,并把这个三位数在纸上写两遍构成一个六位数交给B同学,如他心里想的是789,那么他在纸上写的就是789789,B把这个六位数除以7,得到的商写在另一张纸上并交给C同学,C同学把B同学给他的数字除以11,得到的商写在另一张纸上并交给D同学,D同学把C同学给他的数字除以13,得到的商写在另一张纸上,并交还给A同学,还给![]() 同学的数字和他刚开始想的数字有什么关系?并说明理由.
同学的数字和他刚开始想的数字有什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
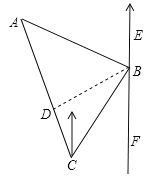
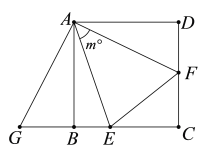
【题目】如图,已知正方形![]() 的边长是
的边长是![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() 于点
于点![]() ,
,![]() 是
是![]() 延长线上一点,且始终保持
延长线上一点,且始终保持![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当![]() 时:
时:
①求![]() 的值;②若
的值;②若![]() 是
是![]() 的中点,求
的中点,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
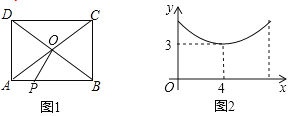
【题目】如图1,在长方形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点O,动点P从点A出发,沿
交于点O,动点P从点A出发,沿![]() 匀速运动,到达点B时停止,设点P所走的路程为x.线段
匀速运动,到达点B时停止,设点P所走的路程为x.线段![]() 的长为y,若y与x之间的函数图象如图2所示,图象与y轴的交点为E.则E的纵坐标为_______________,则长方形
的长为y,若y与x之间的函数图象如图2所示,图象与y轴的交点为E.则E的纵坐标为_______________,则长方形![]() 的周长为____________.
的周长为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com