
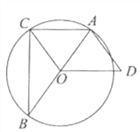
【题目】如图,已知△ABC内接于![]() ,AB是直径,OD∥AC,AD=OC.
,AB是直径,OD∥AC,AD=OC.
(1)求证:四边形OCAD是平行四边形;
(2)填空:①当∠B= 时,四边形OCAD是菱形;
②当∠B= 时,AD与![]() 相切.
相切.
【答案】(1)证明见解析;(2)① 30°,② 45°
【解析】试题分析:(1)根据已知条件求得∠OAC=∠OCA,∠AOD=∠ADO,然后根据三角形内角和定理得出∠AOC=∠OAD,从而证得OC∥AD,即可证得结论;
(2)①若四边形OCAD是菱形,则OC=AC,从而证得OC=OA=AC,得出∠![]() 即可求得
即可求得![]()
②AD与![]() 相切,根据切线的性质得出
相切,根据切线的性质得出![]() 根据AD∥OC,内错角相等得出
根据AD∥OC,内错角相等得出![]() 从而求得
从而求得![]()
试题解析:(方法不唯一)
(1)∵OA=OC,AD=OC,
∴OA=AD,
∴∠OAC=∠OCA,∠AOD=∠ADO,
∵OD∥AC,
∴∠OAC=∠AOD,
∴∠OAC=∠OCA=∠AOD=∠ADO,
∴∠AOC=∠OAD,
∴OC∥AD,
∴四边形OCAD是平行四边形;
(2)①∵四边形OCAD是菱形,
∴OC=AC,
又∵OC=OA,
∴OC=OA=AC,
∴![]()
∴![]()
故答案为: ![]()
②∵AD与![]() 相切,
相切,
∴![]()
∵AD∥OC,
∴![]()
∴![]()
故答案为: ![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点0为直线AB上一点,∠AOC=50![]() ,OD平分∠AOC,∠DOE=90
,OD平分∠AOC,∠DOE=90![]() .
.
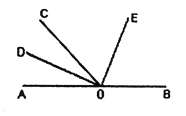
(1)请你数一数,图中有多少个小于平角的角:
(2)求出∠BOD的度数;
(3)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在3月份举行读书节活动,鼓励学生进行有益的课外阅读,张老师为了了解该校学生课外阅读的情况,设计了“你最喜欢的课外读物类型”的调查问卷,包括“名著”“科幻”“历史”“童话”四类,在学校随机抽取了部分学生进行调查,被抽取的学生只能在四种类型中选择其中一类,最后将调查结果绘制成如下两幅尚不完整的统计图.
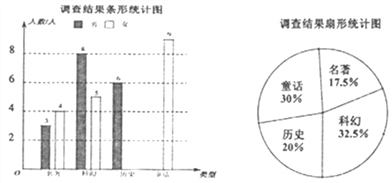
请你根据以上信息解答下列问题:
(1)本次调查中,张老师一共调查了 名学生;
(2)求本次调查中选择“历史”类的女生人数和“童话”类的男生人数,并将条形统计图补充完整;
(3)扇形图中“童话”类对应的圆心角度数为 .
(4)如果该校共有学生360名,请估算该校最喜欢“名著”类和“历史”类的学生总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.

(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
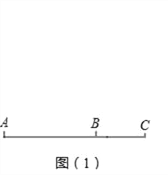
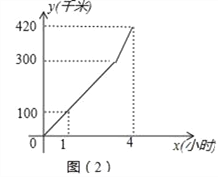
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
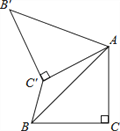
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com