
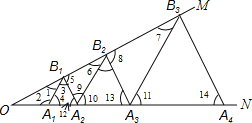
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为_____.

【答案】64
【解析】
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2…进而得出答案.
解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:A7B7=64B1A2=64.
故答案是:64


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
… …
按照上述规律排下去,那么第10行从左边数第5个数等于
A.50B.-50C.60D.-60
查看答案和解析>>
科目:初中数学 来源: 题型:
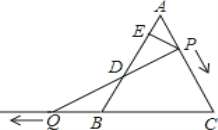
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
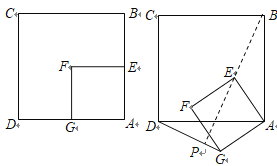
【题目】如图,正方形ABCD和正方形AEFG,边AE在边AB上,AB=2AE=2.将正方形AEFG绕点A逆时针旋转60°,BE的延长线交直线DG于点P ,旋转过程中点P运动的路线长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
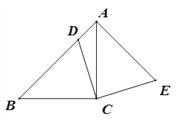
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连结CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
(1)求证:AB⊥AE;
(2)若![]() ,求证:四边形ADCE为正方形.
,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一块瓷砖的图案用这种瓷砖来铺设地面如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个15×15的正方形图案,则其中完整的圆共有( )个.
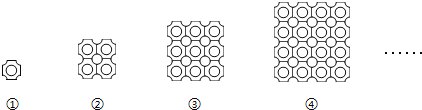
A.365B.366C.420D.421
查看答案和解析>>
科目:初中数学 来源: 题型:
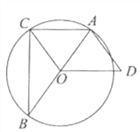
【题目】如图,已知△ABC内接于![]() ,AB是直径,OD∥AC,AD=OC.
,AB是直径,OD∥AC,AD=OC.
(1)求证:四边形OCAD是平行四边形;
(2)填空:①当∠B= 时,四边形OCAD是菱形;
②当∠B= 时,AD与![]() 相切.
相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正方体的六个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问:长方体的下底面共有多少朵花?
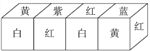
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一振子从点A开始左右来回振动8次,如果规定向右为正,向左为负,这8次振动的记录为(单位:mm):+10,-9,+8,-6,+7.5,-6,+8,-7.
(1)求该振子停止时所在的位置距A点多远?
(2)如果每毫米需用时间0.02 s,则完成8次振动共需要多少秒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com