
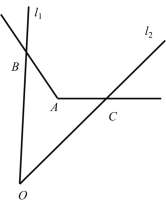
【题目】(1)如图①,直线AB//CD,试确定∠B,∠BPC,∠C之间的数量关系:
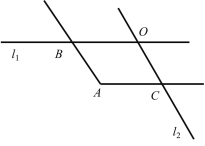
(2)如图②,直线AB//CD.∠ABP与∠DCP的平分线相交于点P1,请确定∠P与∠P1的数量关系;
(3)如图③,若∠A=![]() (0<
(0<![]() <180°,且
<180°,且![]() ≠135°),点B点C分别在∠A的两边上,分别过点B和点C作直线
≠135°),点B点C分别在∠A的两边上,分别过点B和点C作直线![]() 和
和![]() .使得,
.使得,![]() 、
、![]() 分别与AB,AC的夹角为
分别与AB,AC的夹角为![]() .且
.且![]() 和
和![]() 交于点O,请直接写出∠BOC的度数.
交于点O,请直接写出∠BOC的度数.

【答案】(1)![]() ,见解析;(2)
,见解析;(2)![]() ,见解析;
,见解析;
(3)∠BOC=3∠α-360°,或∠BOC=∠α,或∠BOC=180°-∠α.
【解析】
(1)过P作AB的平行线PQ,根据平行线的性质得出关系;
(2)利用角平分线的性质和平行线中角的关系可得;
(3)画出示意图,结合利用外角的性质可得结论
解:(1)过P作AB的平行线PQ,则PQ∥AB∥CD,
∴∠B=∠BPQ,∠CPQ+∠C=180,
∴![]()
(2)由题意可得:
∠P=∠ABP+∠DCP,
∵P1B 和P1C分别是∠ABP与∠DCP的平分线,
∴∠AB P1=∠PB P1,∠DC P1=∠PC P1,
∵∠P1=∠AB P1+∠DC P1,
∴![]() .
.
(3)如下三图,分别为:
∠BOC=3∠α-360°,或∠BOC=∠α,或∠BOC=180°-∠α.



 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】为了了解我市中学生跳绳活动开展的情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制成如下的两个不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?请补全频数分布直方图;
(2)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀;
(3)请你根据以上信息,对我市开展的学生跳绳活动情况谈谈自己的看法或建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒。
(1)当t=3秒时,求△ABP的面积;
(2)当t为何值时,点P与点A的距离为5cm?
(3)当t为何值时(2<t<5),以线段AD、CP、AP的长度为三角形是直角三角形,且AP是斜边。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
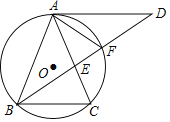
【题目】如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)求∠DAF的度数;
(2)求证:AE2=EFED;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示,慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段OC所示,根据图像进行以下研究:


(1)甲、乙两地之间的距离为 km;线段AB的解析式为 ;线段OC的解析式为 ;
(2)经过多长时间,快慢车相距50千米?
(3)设快、慢车之间的距离为y(km),并画出函数的大致图像.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大妈加盟了“红红”全国烧烤连锁店,该公司的宗旨是“薄利多销”,经市场调查发现,当羊肉串的单价定为![]() 元时,每天能卖出
元时,每天能卖出![]() 串,在此基础上,每加价
串,在此基础上,每加价![]() 元李大妈每天就会少卖出
元李大妈每天就会少卖出![]() 串,考虑了所有因素后李大妈的每串羊肉串的成本价为
串,考虑了所有因素后李大妈的每串羊肉串的成本价为![]() 元,若李大妈每天销售这种羊肉串想获得利润是
元,若李大妈每天销售这种羊肉串想获得利润是![]() 元,那么请问这种羊肉串应怎样定价?
元,那么请问这种羊肉串应怎样定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
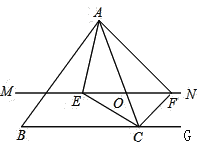
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
(3)当点![]() 运动到何处,且
运动到何处,且![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com