
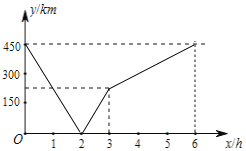
【题目】一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示,慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段OC所示,根据图像进行以下研究:


(1)甲、乙两地之间的距离为 km;线段AB的解析式为 ;线段OC的解析式为 ;
(2)经过多长时间,快慢车相距50千米?
(3)设快、慢车之间的距离为y(km),并画出函数的大致图像.
【答案】(1)450, y1=﹣150x+450,y2=75x;(2)当经过![]() 、
、![]() 小时,快慢车相距50千米;(3)见解析
小时,快慢车相距50千米;(3)见解析
【解析】
(1)利用A点坐标为(0,450),可以得出甲,乙两地之间的距离,B点坐标为(3,0),代入y1=kx+b求出即可,利用线段OC解析式为y2=ax 求出a即可;
(2)分两种情况考虑:y1﹣y2=50,y2﹣y1=50,得出方程求解即可;
(3)利用(2)中所求得出,y=|y1-y2|进而求出函数解析式,得出图象即可.
(1)由图象可得,
甲、乙两地之间的距离为450km
设线段AB对应的函数解析式为y1=kx+b,
![]() ,得
,得![]() ,
,
即线段AB对应的函数解析式为y1=﹣150x+450,
设线段OC对应的函数解析式为y2=ax,
450=6a,得a=75,
即线段OC对应的函数解析式为y2=75x,
(2) y1﹣y2=50,即﹣150x+450-75x=50,![]()
y2﹣y1=50,即75x﹣(﹣150x+450)=50,![]()
当经过![]() 、
、![]() 小时,快慢车相距50千米
小时,快慢车相距50千米
(3)甲车的速度为:450÷3=150km/h,乙车的速度为:450÷6=75km/h,
故甲乙两车相遇的时间为:450÷(150+75)=2h,
设快、慢车之间的距离为y(km),这个函数的大致图象如右图所示.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(9分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与y轴交于点C.
,与y轴交于点C.
(1)![]() = ,
= ,![]() = ;
= ;
(2)根据函数图象可知,当![]() >
>![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当![]() :
:![]() =3:1时,求点P的坐标.
=3:1时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
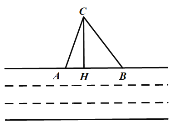
【题目】笔直的河流一侧有一旅游地C,河边有两个漂流点A.B.其中AB=AC,由于某种原因,由C到A的路现在已经不通,为方便游客决定在河边新建一个漂流点H(A,H,B在一条直线上),并新修一条路CH测得BC=5千米,CH=4干米,BH=3千米,
(1)问CH是否为从旅游地C到河的最近的路线?请通过计算加以说明;
(2)求原来路线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,直线AB//CD,试确定∠B,∠BPC,∠C之间的数量关系:
(2)如图②,直线AB//CD.∠ABP与∠DCP的平分线相交于点P1,请确定∠P与∠P1的数量关系;
(3)如图③,若∠A=![]() (0<
(0<![]() <180°,且
<180°,且![]() ≠135°),点B点C分别在∠A的两边上,分别过点B和点C作直线
≠135°),点B点C分别在∠A的两边上,分别过点B和点C作直线![]() 和
和![]() .使得,
.使得,![]() 、
、![]() 分别与AB,AC的夹角为
分别与AB,AC的夹角为![]() .且
.且![]() 和
和![]() 交于点O,请直接写出∠BOC的度数.
交于点O,请直接写出∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班组织了一次食品安全知识竞赛,甲、乙两队各5人的成绩如表所示(10分制).
数据 | 中位数 | 众数 | 方差 | |||||
甲 | 8 | 10 | 9 | 6 | 9 | 9 | 1.84 | |
乙 | 10 | 8 | 9 | 7 | 8 | 8 | 1.04 | |
(1)补全表格中的众数和中位数
(2)并判断哪队的成绩更稳定?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们设[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1-m,-1-m]的函数的若干结论:
①当m=-3时,该函数图象的顶点坐标是(![]() ,
,![]() );
);
②当m=1时,该函数图象截x轴所得的线段的长度为2;
③当m=-1时,该函数在x>![]() 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,该函数图象必经过x轴上的一个定点.
上述结论中正确的有_________________.(只需填写所有正确答案的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
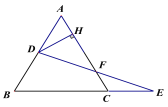
【题目】如图,已知等边三角形ABC的边长为7,点D为AB上一点,点E在BC的延长线上,且CE=AD,连接DE交AC于点F,作DH⊥AC于点H,则线段HF的长为 ____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:把![]() 和
和![]() 按如图甲摆放(点
按如图甲摆放(点![]() 与点
与点![]() 重合),点
重合),点![]() 、
、![]() 、
、![]() 在同一条直线上.
在同一条直线上.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如图乙,
.如图乙,![]() 从图甲的位置出发,以
从图甲的位置出发,以![]() 的速度沿
的速度沿![]() 向
向![]() 匀速移动,在
匀速移动,在![]() 移动的同时,点
移动的同时,点![]() 从
从![]() 的顶点
的顶点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动.当点
匀速移动.当点![]() 移动到点
移动到点![]() 时,
时,![]() 点停止移动,
点停止移动,![]() 也随之停止移动.
也随之停止移动.![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() 、
、![]() ,设移动时间为
,设移动时间为![]() .解答下列问题:
.解答下列问题:
![]() 设三角形
设三角形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 当
当![]() 为何值时,三角形
为何值时,三角形![]() 为等腰三角形?
为等腰三角形?
![]() 是否存在某一时刻
是否存在某一时刻![]() ,使
,使![]() 、
、![]() 、
、![]() 三点在同一条直线上?若存在,求出此时
三点在同一条直线上?若存在,求出此时![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com