
【题目】如图,二次函数的图象与![]() 轴交于点
轴交于点![]() ,
,![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() ,
,![]() 是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点
是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点![]() ,
,![]() .
.

![]() 请直接写出点
请直接写出点![]() 的坐标;
的坐标;
![]() 求二次函数的解析式;
求二次函数的解析式;
![]() 根据图象直接写出一次函数值大于二次函数值的
根据图象直接写出一次函数值大于二次函数值的![]() 的取值范围.
的取值范围.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
【题目】已知x=1是一元二次方程(m+1)x-mx+2m+3=0的一个根。
(1)求m的值,并写出此时的一元二次方程的一般形式
(2)把方程两根分别记为![]() ,
,![]() ,不解方程,求
,不解方程,求![]() +
+![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
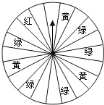
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购物满
份),并规定:顾客每购物满![]() 元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得![]() 元的购物券.
元的购物券.
![]() 求转动一次转盘获得购物券的概率;
求转动一次转盘获得购物券的概率;
![]() 转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,其对称轴为
的图象如图所示,其对称轴为![]() ,则正确的结论是( )
,则正确的结论是( )

A. abc>0 B. 3a+c<0
C. 4a+2b+c<0 D. b2-4ac<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AC=10,S△ABC =25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是( )

A. 4 B. ![]() C. 5 D. 6
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海珠区某学校为进一步加强和改进学校体育工作,切实提高学生体质健康水平,决定推进“一人一球”活动计划. 学生可根据自己的喜好选修一门球类项目(A :足球,B:篮球,C:排球,D:羽毛球,E:乒乓球),陈老师对某班全班同学的
选课情况进行统计后,制成了两幅不完整的统计图 (如图).
(1) 求出该班的总人数,并将条形统计图补充完整;
(2) 若该校共有学生 2500 名,请估计约有多少人选修足球?
(3) 该班班委 4 人中,1 人选修足球,1 人选修篮球,2 人选修羽毛球,陈老师要从这
4 人中任选 2 人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求 选出的 2 人中至少有 1 人选修羽毛球的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年中秋节来期间,某超市以每盒80元的价格购进了1000盒月饼,第一周以每盒168元的价格销售了300盒,第二周如果单价不变,预计仍可售出300盒,该超市经理为了增加销量,决定降价,据调查,单价每降低1元,可多售出10盒,但最低每盒要赢利30元,第二周结束后,该超市将对剩余的月饼一次性赔钱甩卖,此时价格为70元/盒.
(1)若设第二周单价降低x元,则第二周的单价是 ______ ,销量是 ______ ;
(2)经两周后还剩余月饼 ______ 盒;
(3)若该超市想通过销售这批月饼获利51360元,那么第二周的单价应是多元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com