
【题目】已知x=1是一元二次方程(m+1)x-mx+2m+3=0的一个根。
(1)求m的值,并写出此时的一元二次方程的一般形式
(2)把方程两根分别记为![]() ,
,![]() ,不解方程,求
,不解方程,求![]() +
+![]() 的值。
的值。
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.

(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x-k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
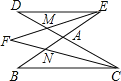
【题目】如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.
(1)若∠D=70°,∠BED=30°,则∠EMA= (度);
(2)若∠B=60°,∠BCD=40°,则∠ENC= (度);
(3)∠F与∠B、∠D有怎样的数量关系?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②DE长度的最小值为4;③四边形CDFE的面积保持不变;④△CDE面积的最大值为8.其中正确的结论是( )
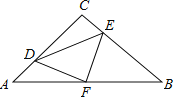
A.①②③B.①③C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
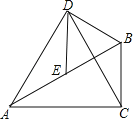
(1)求证:△ADE≌△CDB;
(2)若BC=1,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠BAC=90°,AD⊥BC 于 D,BE 平分∠ABC 交 AC 于 E, 交 AD 于 F,FG∥BC,FH∥AC,下列结论:①AE=AF;②ΔABF≌ΔHBF;③AG=CE;④AB+FG=BC,其中正确的结论有()

A.①②③B.①③④C.①②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
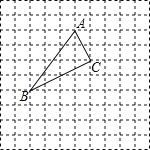
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与![]() 轴交于点
轴交于点![]() ,
,![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() ,
,![]() 是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点
是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点![]() ,
,![]() .
.

![]() 请直接写出点
请直接写出点![]() 的坐标;
的坐标;
![]() 求二次函数的解析式;
求二次函数的解析式;
![]() 根据图象直接写出一次函数值大于二次函数值的
根据图象直接写出一次函数值大于二次函数值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com