
【题目】如图,在 Rt△ABC 中,∠BAC=90°,AD⊥BC 于 D,BE 平分∠ABC 交 AC 于 E, 交 AD 于 F,FG∥BC,FH∥AC,下列结论:①AE=AF;②ΔABF≌ΔHBF;③AG=CE;④AB+FG=BC,其中正确的结论有()

A.①②③B.①③④C.①②③④D.①②④
【答案】C
【解析】
只要证明∠AFE=∠AEF,四边形FGCH是平行四边形,△FBA≌△FBH即可解决问题;
解:∵∠FBD=∠ABF,∠FBD+∠BFD=90°,∠ABF+∠AEB=90°,
∴∠BFD=∠AEB,
∴∠AFE=∠AEB,
∴AF=AE,故①正确,
∵FG∥BC,FH∥AC,
∴四边形FGCH是平行四边形,
∴FH=CG,FG=CH,∠FHD=∠C,
∵∠BAD+∠DAC=90°,∠DAC+∠C=90°,
∴∠BAF=∠BHF,
∵BF=BF,∠FBA=∠FBH,
∴△FBA≌△FBH,
∴FA=FH,故AB=BH,②正确,
∵AF=AE,FH=CG,
∴AE=CG,
∴AG=CE,故③正确,
∵BC=BH+HC,BH=BA,CH=FG,
∴BC=AB+FG,故④正确.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(2015本溪,第9题,3分)如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线![]() (
(![]() )上,则k的值为( )
)上,则k的值为( )

A. 4 B. ﹣2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片![]() 纸沿对角线折叠,设重叠部分为△
纸沿对角线折叠,设重叠部分为△![]() ,那么,下列说法错误的是( )
,那么,下列说法错误的是( )
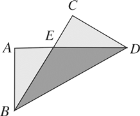
A.△![]() 是等腰三角形,
是等腰三角形,![]()
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=1是一元二次方程(m+1)x-mx+2m+3=0的一个根。
(1)求m的值,并写出此时的一元二次方程的一般形式
(2)把方程两根分别记为![]() ,
,![]() ,不解方程,求
,不解方程,求![]() +
+![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购物满
份),并规定:顾客每购物满![]() 元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得![]() 元的购物券.
元的购物券.
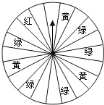
![]() 求转动一次转盘获得购物券的概率;
求转动一次转盘获得购物券的概率;
![]() 转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海珠区某学校为进一步加强和改进学校体育工作,切实提高学生体质健康水平,决定推进“一人一球”活动计划. 学生可根据自己的喜好选修一门球类项目(A :足球,B:篮球,C:排球,D:羽毛球,E:乒乓球),陈老师对某班全班同学的
选课情况进行统计后,制成了两幅不完整的统计图 (如图).
(1) 求出该班的总人数,并将条形统计图补充完整;
(2) 若该校共有学生 2500 名,请估计约有多少人选修足球?
(3) 该班班委 4 人中,1 人选修足球,1 人选修篮球,2 人选修羽毛球,陈老师要从这
4 人中任选 2 人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求 选出的 2 人中至少有 1 人选修羽毛球的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com