
【题目】如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
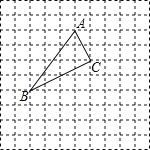
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
(4)求△ABC的面积.
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=10![]() cm,设OE=x,求x值及阴影部分的面积.
cm,设OE=x,求x值及阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=1是一元二次方程(m+1)x-mx+2m+3=0的一个根。
(1)求m的值,并写出此时的一元二次方程的一般形式
(2)把方程两根分别记为![]() ,
,![]() ,不解方程,求
,不解方程,求![]() +
+![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强校园阳光体育活动,某中学计划购进一批篮球和排球,经过调查得知每个篮球的价格比每个排球的价格贵40元,买5个篮球和10个排球共用1100元.
(1)求每个篮球和排球的价格分别是多少?
(2)某学校需购进篮球和排球共120个,总费用不超过9000元,但不低于8900元,问有几种购买方案?最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
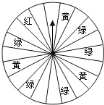
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购物满
份),并规定:顾客每购物满![]() 元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得![]() 元的购物券.
元的购物券.
![]() 求转动一次转盘获得购物券的概率;
求转动一次转盘获得购物券的概率;
![]() 转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,其对称轴为
的图象如图所示,其对称轴为![]() ,则正确的结论是( )
,则正确的结论是( )

A. abc>0 B. 3a+c<0
C. 4a+2b+c<0 D. b2-4ac<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年中秋节来期间,某超市以每盒80元的价格购进了1000盒月饼,第一周以每盒168元的价格销售了300盒,第二周如果单价不变,预计仍可售出300盒,该超市经理为了增加销量,决定降价,据调查,单价每降低1元,可多售出10盒,但最低每盒要赢利30元,第二周结束后,该超市将对剩余的月饼一次性赔钱甩卖,此时价格为70元/盒.
(1)若设第二周单价降低x元,则第二周的单价是 ______ ,销量是 ______ ;
(2)经两周后还剩余月饼 ______ 盒;
(3)若该超市想通过销售这批月饼获利51360元,那么第二周的单价应是多元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com