
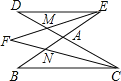
【题目】如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.
(1)若∠D=70°,∠BED=30°,则∠EMA= (度);
(2)若∠B=60°,∠BCD=40°,则∠ENC= (度);
(3)∠F与∠B、∠D有怎样的数量关系?证明你的结论.
【答案】(1)85;(2)80;(3)∠F=![]() (∠B+∠D).
(∠B+∠D).
【解析】
(1)利用角平分线的性质以及三角形外角的性质求解即可;
(2)利用角平分线的性质以及三角形外角的性质求解即可;
(3)利用三角形外角的性质求得∠D+∠DEF+∠B+∠BCF=∠F+∠DCF+∠F+∠BEF,利用角平分线的性质可证得∠B+∠D=2∠F,从而求得答案.
(1)∵EF为∠BED的平分线,∠BED=30°,
∴∠DEM=∠FEN=![]() ∠BED=15°.
∠BED=15°.
又∵∠EMA=∠D+∠DEM,∠D=70°,
∴∠EMA=85°.
故答案为:85°.
(2)∵CF为∠BCD的平分线,∠BCD=40°,
∴∠BCN=∠FCM=![]() ∠BCD=20°.
∠BCD=20°.
又∵∠ENC=∠B+∠BCN,∠B=60°,
∴∠ENC=80°.
故答案为:80°.
(3)∠F=![]() (∠B+∠D).
(∠B+∠D).
证明:∵∠EMA=∠D+∠DEF=∠F+∠DCF,
∠ENC=∠B+∠BCF=∠F+∠BEF,
∴∠D+∠DEF+∠B+∠BCF=∠F+∠DCF+∠F+∠BEF.
又∵CF为∠BCD的平分线,EF为∠BED的平分线,
∴∠DEF=∠BEF,∠DCF=∠BCF.
∴∠B+∠D=2∠F.
即:∠F=![]() (∠B+∠D).
(∠B+∠D).


科目:初中数学 来源: 题型:
【题目】(2015本溪,第9题,3分)如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线![]() (
(![]() )上,则k的值为( )
)上,则k的值为( )

A. 4 B. ﹣2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=10![]() cm,设OE=x,求x值及阴影部分的面积.
cm,设OE=x,求x值及阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
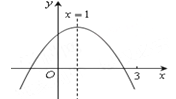
【题目】二次函数![]() (a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>
(a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>![]() ;④a-b+c>0;⑤若
;④a-b+c>0;⑤若![]() , 且
, 且![]() , 则
, 则![]() .其中正确的有( ).
.其中正确的有( ).
A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠B=60°,∠ADC=90°,∠BCD=150°,点E是AB边上一点,DE⊥AB,EC⊥BC.

(1)试判断△DEC的形状,并说明理由.
(2)若BC=3,BE=6.求AB和AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
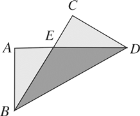
【题目】如图,把长方形纸片![]() 纸沿对角线折叠,设重叠部分为△
纸沿对角线折叠,设重叠部分为△![]() ,那么,下列说法错误的是( )
,那么,下列说法错误的是( )
A.△![]() 是等腰三角形,
是等腰三角形,![]()
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=1是一元二次方程(m+1)x-mx+2m+3=0的一个根。
(1)求m的值,并写出此时的一元二次方程的一般形式
(2)把方程两根分别记为![]() ,
,![]() ,不解方程,求
,不解方程,求![]() +
+![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
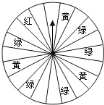
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购物满
份),并规定:顾客每购物满![]() 元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得![]() 元的购物券.
元的购物券.
![]() 求转动一次转盘获得购物券的概率;
求转动一次转盘获得购物券的概率;
![]() 转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com