
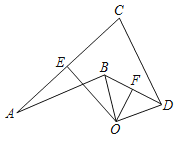
【题目】如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点.
的图象交于A(2,3),B(6,n)两点.
(1)分别求出一次函数与反比例函数的解析式;
(2)求△OAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
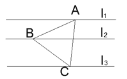
【题目】如图所示,l1∥l2∥l3,l1、l2间的距离为3, l2、l3间的距离为6,等边△ABC三个顶点均在l1、l2、l3上,则△ABC的边长为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2.要在这张纸板中剪出一个尽可能大的正方形(剪法如图1所示),图1中剪法称为第1次剪取,记所得的正方形面积为S1;按照图1中的剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为S2(如图2),则S2=_____;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形的面积和为S3(如图3);继续操作下去…则第2018次剪取后,S2018=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
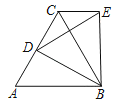
【题目】如图,点D是等边△ABC的边AC上一点,以BD为边作等边△BDE,点C,E在BD同侧,下列结论:①∠ABD=30°;②CE∥AB;③CB平分∠ACE;④CE=AD,其中错误的有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.

(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,△PBQ的面积能否等于8cm2?
(3)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于5cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.

(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x-k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
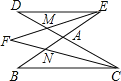
【题目】如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.
(1)若∠D=70°,∠BED=30°,则∠EMA= (度);
(2)若∠B=60°,∠BCD=40°,则∠ENC= (度);
(3)∠F与∠B、∠D有怎样的数量关系?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com