练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．已知|x-12|+|z-13|+y2-10y+25=0，则以x、y、z为三边的三角形是直角三角形．

    分析 先根据非负数的性质求出x、y、z的值，再根据勾股定理的逆定理进行解答即可．

    解答 解：以x，y，z为三边的三角形是直角三角形．
    ∵|x-12|+|z-13|+y2-10y+25=0，
    ∴|x-12|+|z-13|+（y-5）2=0，
    ∴x-12=0，z-13=0，y-5=0，
    ∴x=12，y=5，z=13，
    ∵122+52=132，
    ∴以x，y，z为三边的三角形是直角三角形．
    故答案为直角．

    点评 本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

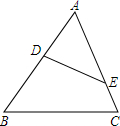    10．如图，在△ABC中，∠ADE=∠C，那么下列等式中，成立的是（　　）
    A．$\frac{DE}{BC}$=$\frac{AE}{AB}$B．$\frac{AE}{BC}$=$\frac{AD}{BD}$C．$\frac{AD}{AB}$=$\frac{AE}{AC}$D．$\frac{DE}{BC}$=$\frac{AD}{AB}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．下列哪个方程是一元二次方程（　　）
    A．x+2y=1B．2x（x-1）-2x+3=0C．$\frac{1}{{x}^{2}}$+4x=3D．x2-2xy=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列各数-$\frac{{3}^{2}}{4}$，0，（-$\frac{1}{2}$）2，3.14159，π，|-3.4|中，正分数有（　　）
    A．3个B．4个C．5个D．6个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．将代数式x2+6x+3配方成（x+m）2+n的形式，则m-n=9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．对于实数x，我们规定[x）表示大于x的最小整数，如[4）=5，[$\sqrt{3}$）=2，[-2.5）=-2，现对64进行如下操作：64$\stackrel{第1次}{→}$[$\sqrt{64}$）=9$\stackrel{第2次}{→}$[$\sqrt{9}$）=4$\stackrel{第3次}{→}$[$\sqrt{4}$）=3$\stackrel{第4次}{→}$[$\sqrt{3}$）=2，这样对64只需进行4次操作后变为2，类似地，只需进行4次操作后变为2的所有正整数中，最大的是3968．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如果单项式xa+5y与2x3yb-1是同类项，那么ab=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．一副扑克牌54张牌，从中任抽一张牌，抽到大王或小王的概率为（　　）
    A．$\frac{1}{54}$B．$\frac{1}{27}$C．$\frac{1}{9}$D．$\frac{1}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列说法正确的是（　　）
    A．带根号的数都是无理数B．无理数一定是无限不循环小数
    C．无理数与无理数的和是无理数D．有理数与无理数的积是无理数

    查看答案和解析>>

    同步练习册答案