
分析 先分别根据∠AOB与∠BOC在边OB的同侧和∠AOB与∠BOC在边OB的两侧画出图形,然后根据角平分线的定义以及角的和差关系进行计算即可.
解答 解:当∠AOB与∠BOC在边OB的同侧时,如图1所示: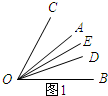
因为OD平分∠AOB,所以∠BOD=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×40°=20°
又因为OE平分∠BOC,所以∠BOE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×60°=30°
所以有∠DOE=∠BOE-∠BOD=30°-20°=10°;
当∠AOB与∠BOC在边OB的两侧时,如图2所示: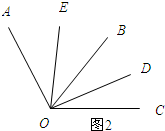
此时,因为OD平分∠AOB,所以∠BOD=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×40°=20°
又因为OE平分∠BOC,所以∠BOE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×60°=30°
所以有∠DOE=∠BOE+∠BOD=30°+20°=50°
综上所述:∠DOE为10°或50°.
点评 本题主要考查的是角平分线的定义,根据题意分类画出图形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
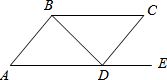 如图,点E在AD的延长线上,下列条件中能使AB∥CD的是( )
如图,点E在AD的延长线上,下列条件中能使AB∥CD的是( )| A. | ∠ABD=∠CDB | B. | ∠ADB=∠CBD | C. | ∠C=∠CDE | D. | ∠C+∠ADC=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
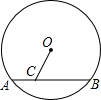 如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )
如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )| A. | $\sqrt{13}$ | B. | 3 | C. | 4 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
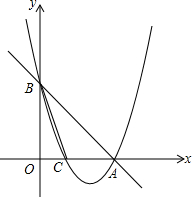 已知:如图直线y=-x+6与x轴、y轴分别交于A、B两点.抛物线y=$\frac{1}{2}$x2+bx+c过A、B两点,与x轴的另一个交点为C点.
已知:如图直线y=-x+6与x轴、y轴分别交于A、B两点.抛物线y=$\frac{1}{2}$x2+bx+c过A、B两点,与x轴的另一个交点为C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
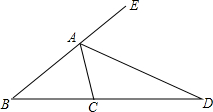 如图,已知△ABC中,AD是△ABC外角平分线,交BC延长线于D,求证:$\frac{AB}{AC}$=$\frac{BD}{DC}$.
如图,已知△ABC中,AD是△ABC外角平分线,交BC延长线于D,求证:$\frac{AB}{AC}$=$\frac{BD}{DC}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任何数与0相乘都得0 | B. | 0是最小的有理数 | ||
| C. | 绝对值最小的有理数是0 | D. | 0没有倒数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com