
分析 由于第14个数并不是太大,因此,观察规律,从第六个数开始,每个数等于它的前三个数之和减去前一个数,依次往后列举出第14个数.
解答 解:从第六个数开始,每个数等于它的前三个数之和减去前一个数:
第6个:4=2+2,
第7个:5=2+3,
第8个:7=3+4,
第9个:9=4+5,
第10个:12=5+7,
第11个:16=7+9,
第12个:21=9+12,
第13个:28=12+16,
第14个:37=16+21,
即:第14个数为37.
点评 本题以数列的形式考查了数字变化的规律,属基础题.数字规律的探究题是最近中考的热点,着重考查学生的观察能力、归纳分析能力,这就要求学生在已有知识的基础上进行发散性思考,充分联想,进而总结出规律.


科目:初中数学 来源: 题型:解答题
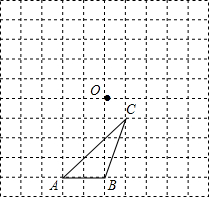 如图所示,△ABC与点O在10×10的网格中的位置如图所示
如图所示,△ABC与点O在10×10的网格中的位置如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
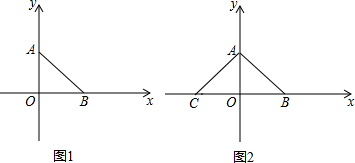
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
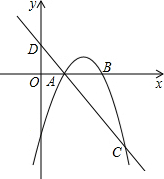 如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).
如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com