
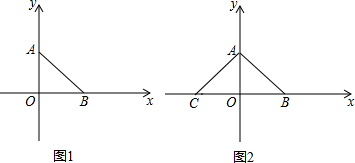
���� ��1��������֪�����õ�OA=OB�����ù��ɶ������OA=OB=2�����������ε������ʽ���ɽ��
��2����ͼ2������P��PN��AC�ڵ�N������D��DM��BC�ڵ�M���ɡ�ANP�ס�PMD�����Ʊ�Ϊ$\sqrt{2}$��1���õ�$\frac{AN}{PM}=\frac{PN}{DM}=\frac{\sqrt{2}}{1}$����OP=t�����PM=2-$\frac{t}{2}$��DM=$\frac{t}{2}$���õ�OM=PM-OP=2-$\frac{t}{2}$-��2-t��=$\frac{t}{2}$������D��$\frac{t}{2}��\frac{t}{2}$����
��3�����ɵ�E�ǵ�D����AP�ĶԳƵ㣬�õ���APD=��APE=45�㣬���PD=AD����OP=OD�����EPO=��ODA�����AOD�ա�EOP��SAS������OP=ODʱ����3��������������2-t=$\frac{\sqrt{2}}{2}$t�����t=4-2$\sqrt{2}$����ͼ3������E��EK��BC�����EPK�ա�PDM���õ�EK=PM��PK=DM=2-$\sqrt{2}$�����PM=$\sqrt{2}$������EK=PM=OK������EK=$\sqrt{2}$���Ӷ��õ�E��-$\sqrt{2}$��$\sqrt{2}$����
��� �⣺��1���ߡ�OAB=45�㣬��AOB=90�㣬
���OAB=��OBA��
��OA=OB��
��AB=2$\sqrt{2}$��
��OA=OB=2��
��${S}_{��AOB}=\frac{1}{2}��2��2$=2��
��2����ͼ2������P��PN��AC�ڵ�N������D��DM��BC�ڵ�M��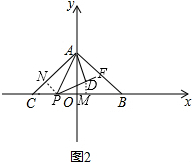
�ɡ�ANP�ס�PMD�����Ʊ�Ϊ$\sqrt{2}$��1��
��$\frac{AN}{PM}=\frac{PN}{DM}=\frac{\sqrt{2}}{1}$��
��OP=t��
�ߡ�ACO=45�㣬PN=$\frac{\sqrt{2}}{2}$t��CN=$\frac{\sqrt{2}}{2}$t��
AN=AC-CN=2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$t��
��PM=2-$\frac{t}{2}$��DM=$\frac{t}{2}$��
��OM=PM-OP=2-$\frac{t}{2}$-��2-t��=$\frac{t}{2}$��
��D��$\frac{t}{2}��\frac{t}{2}$����
��3���ߵ�E�ǵ�D����AP�ĶԳƵ㣬
���APD=��APE=45�㣬
���EPF=90�㣬PE=PD��
��PE=AD��
��PD=AD��
��OP=OD�����EPO=��ODA��
��AOD�ա�EOP��SAS����
��OP=ODʱ����3������������
��2-t=$\frac{\sqrt{2}}{2}$t
t=4-2$\sqrt{2}$��
��ͼ3������E��EK��BC�����EPK�ա�PDM��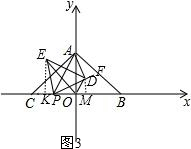
EK=PM��PK=DM=2-$\sqrt{2}$��
��OP=OD=2$\sqrt{2}$-2��
��PM=PO+OM=2$\sqrt{2}$$-2+2-\sqrt{2}$=$\sqrt{2}$��
��EK=PM=OK��
��EK=$\sqrt{2}$��
��E��-$\sqrt{2}$��$\sqrt{2}$����
���� ���⿼���˵���ֱ�������ε����ʡ����ɶ��������������ε��������ж���ȫ�������ε��������ж����������Ĺؼ������������ߣ�����������ȫ�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
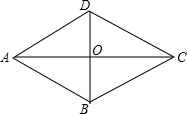 ��ͼ������ABCD���ܳ�Ϊ48cm������һ���Խ���BD��12cm��
��ͼ������ABCD���ܳ�Ϊ48cm������һ���Խ���BD��12cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
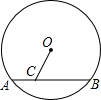 ��ͼ����O�İ뾶Ϊ5����C����AB�ϣ�AC=2��BC=6����OC�ij��ǣ�������
��ͼ����O�İ뾶Ϊ5����C����AB�ϣ�AC=2��BC=6����OC�ij��ǣ�������| A�� | $\sqrt{13}$ | B�� | 3 | C�� | 4 | D�� | 2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{1}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com