
如图,已知P(0,1),⊙P与 轴交于A、B两点,AC是⊙P的直径,OA、OD的长是关于
轴交于A、B两点,AC是⊙P的直径,OA、OD的长是关于 的方程
的方程 的两根,且
的两根,且 。
。
(1)求BC的长;
(2)求证:AD是⊙P的切线;
(3)连结CD交⊙P于点E,过点E作⊙P的切线交 轴于点F,求直线EF的解析式
轴于点F,求直线EF的解析式
 |
(1)解:∵ ,
,
∴
又∵ ,
,
∴
(2)证明:由已知得:
∴
∴ ,解得
,解得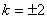
∵
∴ , ∴
, ∴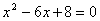
解得,
∴
 法1:可求得:
法1:可求得:
∴
∴
∴AD是⊙P的切线
法2:可求得:直线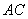 的解析式为
的解析式为 ,
,
直线 的解析式为
的解析式为 (过程略)
(过程略)
∵
∴
∴AD是⊙P的切线
(3)证明:连结AE、PE
法1:∵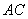 是⊙P的直径 法2:∵
是⊙P的直径 法2:∵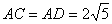 ,
,
∴ ∴
∴
又∵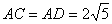 ∴
∴
∴ 是
是 中点 ∴
中点 ∴
∵ ,
, ∵
∵ 是⊙
是⊙ 的切线,
的切线,
∴ , 又∵
, 又∵ ∴
∴
∴ ∴
∴ ∥
∥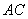
∵ 是⊙
是⊙ 的切线, ∵
的切线, ∵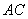 是⊙P的直径
是⊙P的直径
∴ ∴
∴
设直线 的解析式为
的解析式为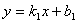 又∵
又∵
直线 的解析式为
的解析式为 ∴
∴ 是
是 中点
中点
可求得 (过程略) ∴
(过程略) ∴ (过程同法1)
(过程同法1)
∵ ∵
∵ ,
, ∥
∥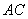
∴ ∴
∴ 是
是 的中点
的中点
∴ ∴
∴
则 设直线
设直线 的解析式为
的解析式为
∴ 可求得:
可求得: (过程略)
(过程略)
∴直线 的解析式为
的解析式为


科目:初中数学 来源: 题型:
 小刚有一块含有30°角的直角三角板,他想测量其短直角边的长度,而手中另外只有一个量角器,于是他采
小刚有一块含有30°角的直角三角板,他想测量其短直角边的长度,而手中另外只有一个量角器,于是他采 用了如下的办法,并获得了相关数据:
用了如下的办法,并获得了相关数据:
第一步,他先用三角板标有刻度的一边测出量角器的直径AB的长度为9cm;
第二步,将三角板与量角器按如图所示的方式摆放,并量得∠BOC为80°(O为AB的中点).
请你根据小刚测得的数据,求出三角板的短直角边AC的长.
(参考数据:sin80°=0.98,cos80°=0.17,tan80°=5.67;sin40°=0.64,cos40°=0.77,tan40°=0.84,结果精确到0.1cm.)
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
下列各式计算正确的个数是( )
①x4·x2=x8;②x3·x3=2x6 ;③a5+a7
;③a5+a7 =a12;
=a12;
④(-a)2·(-a2)=-a4;⑤a4·a3=a7.
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com