
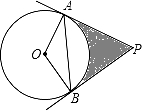
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°,OA=3,则阴影部分面积为 .
9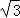 ﹣3π【考点】切线的性质;扇形面积的计算.
﹣3π【考点】切线的性质;扇形面积的计算.
【分析】根据四边形的内角和为360°,根据切线的性质可知:∠OAP=∠OBP=90°,求出∠AOB的度数,进一步求得∠APB的度数,然后根据阴影部分的面积等于四边形OAPB的面积减去扇形AOB的面积即可求得.
【解答】解:∵在△ABO中,OA=OB,∠OAB=30°,
∴∠AOB=180°﹣2×30°=120°,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,
∴在四边形OAPB中,∠APB=360°﹣120°﹣90°﹣90°=60°.
连接OP.
根据切线长定理得∠APO=30°,
∴OP=2OA=6,AP=OP•cos30°=3 ,∠AOP=60°.
,∠AOP=60°.
∴四边形的面积=2S△AOP=2×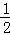 ×3×3
×3×3 =9
=9 ;扇形的面积是
;扇形的面积是 =3π,
=3π,
∴阴影部分的面积是9 ﹣3π.
﹣3π.
故答案为9 ﹣3π.
﹣3π.

【点评】本题考查了切线长定理、切线的性质定理以及30°的直角三角形的性质.关键是熟练运用扇形的面积计算公式,能够把四边形的面积转化为三角形的面积计算..


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
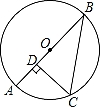
如图,⊙O半径为2,AB为⊙O的直径,BC为⊙O的一条弦,若∠ABC=30°,过点C作AB的垂线,垂足为点D,则CD长为( )
A.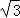 B.
B.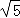 C.2 D.1
C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.
(1)画出△A1OB1,直接写出点A1,B1的坐标;
(2)在旋转过程中,点B经过的路径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
计划在某广场内种植A、B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A、B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木610棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com