
【题目】如图,矩形 ABCD 中,AB=8,BC=6,将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AEFG,AE,FG 分别交射线CD 于点 PH,连结 AH,若 P 是 CH 的中点,则△APH 的周长为( )
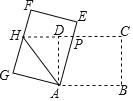
A. 15 B. 18 C. 20 D. 24
【答案】C
【解析】
连结AC,先由△AGH≌△ADH得到∠GHA=∠AHD,进而得到∠AHD=∠HAP,所以△AHP是等腰三角形,所以PH=PA=PC,所以∠HAC是直角,再在Rt△ABC中由勾股定理求出AC的长,然后由△HAC∽△ADC,根据![]() =
=![]() 求出AH的长,再根据△HAC∽△HDA求出DH的长,进而求得HP和AP的长,最后得到△APH的周长.
求出AH的长,再根据△HAC∽△HDA求出DH的长,进而求得HP和AP的长,最后得到△APH的周长.
∵P是CH的中点,PH=PC,∵AH=AH,AG=AD,且AGH与ADH都是直角,∴△AGH≌△ADH,∴∠GHA=∠AHD,又∵GHA=HAP,∴∠AHD=∠HAP,∴△AHP是等腰三角形,∴PH=PA=PC,∴∠HAC是直角,在Rt△ABC中,AC=![]() =10,∵△HAC∽△ADC,∴
=10,∵△HAC∽△ADC,∴![]() =
=![]() ,∴AH=
,∴AH=![]() =
=![]() =7.5,又∵△HAC∽△HAD,
=7.5,又∵△HAC∽△HAD,![]() =
=![]() ,∴DH=4.5,∴HP=
,∴DH=4.5,∴HP=![]() =6.25,AP=HP=6.25,∴△APH的周长=AP+PH+AH=6.25+6.25+7.5=20.
=6.25,AP=HP=6.25,∴△APH的周长=AP+PH+AH=6.25+6.25+7.5=20.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是以∠C为直角的直角三角形,且BC=1,AC=![]() ,圆O是△ABC的外接圆,过△ABC的内角∠C作角平分线交AB于点D,交圆O与点E,连接AE,
,圆O是△ABC的外接圆,过△ABC的内角∠C作角平分线交AB于点D,交圆O与点E,连接AE,
(1)求AE的长.
(2)求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委组织“阳光助残”献爱心捐款活动,九年级(2)班学生捐款如表:
捐款金额(元) | 5 | 10 | 15 | 20 |
人数(人) | 13 | 16 | 17 | 10 |
学生捐款的中位数和众数是( )
A. 10元,15元 B. 15元,15元 C. 10元,20元 D. 16元,17元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,OC OD,OC OD ,DC 的延长线交 y 轴正半轴上点 B ,过点C 作CA BD 交 x 轴负半轴于点A .

(1)如图1,求证:OAOB
(2)如图1,连AD,作OM ∥AC交AD于点M,求证: BC 2OM
(3)如图2,点E为OC 的延长线上一点,连DE,过点D作DFDE且DF DE ,连CF 交 DO 的延长线于点G 若OG 4,求CE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ ABC中,AB = AC

(1)如图 1,如果∠BAD = 30°,AD是BC上的高,AD =AE,则∠EDC =
(2)如图 2,如果∠BAD = 40°,AD是BC上的高,AD = AE,则∠EDC =
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图 3,如果AD不是BC上的高,AD = AE,是否仍有上述关系?如有,请你写出来,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
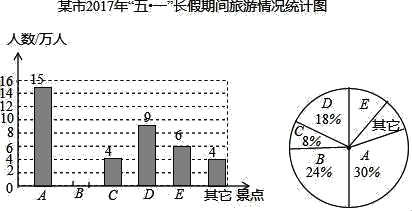
【题目】随着道路交通的不断完善,某市旅游业快速发展,该市旅游景区有A、B、C、D、E等著名景点,市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图(不完整)如下所示,根据相关信息解答下列问题:
(1)2017年“五一”期间,该市旅游景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)在等可能性的情况下,甲、乙两个旅行团在A、B、D三个景点中选择去同一景点的概率是多少?请用画树状图或列表加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每月可卖出
元,每月可卖出![]() 件.市场调查反映:调整价格时,售价每涨
件.市场调查反映:调整价格时,售价每涨![]() 元每月要少卖
元每月要少卖![]() 件;售价每下降
件;售价每下降![]() 元每月要多卖
元每月要多卖![]() 件.为了获得更大的利润,现将饰品售价调整为
件.为了获得更大的利润,现将饰品售价调整为![]() (元/件)(
(元/件)(![]() 即售价上涨,
即售价上涨,![]() 即售价下降),每月饰品销量为
即售价下降),每月饰品销量为![]() (件),月利润为
(件),月利润为![]() (元).
(元).
![]() 直接写出
直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 如何确定销售价格才能使月利润最大?求最大月利润;
如何确定销售价格才能使月利润最大?求最大月利润;
![]() 为了使每月利润不少于
为了使每月利润不少于![]() 元应如何控制销售价格?
元应如何控制销售价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.
(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com