
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌOC ODЃЌOC OD ЃЌDC ЕФбгГЄЯпНЛ y жсе§АыжсЩЯЕу B ЃЌЙ§ЕуC зїCA BD НЛ x жсИКАыжсгкЕуA ЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКOAOB
ЃЈ2ЃЉШчЭМ1ЃЌСЌADЃЌзїOM ЁЮACНЛADгкЕуMЃЌЧѓжЄЃК BC 2OM
ЃЈ3ЃЉШчЭМ2ЃЌЕуEЮЊOC ЕФбгГЄЯпЩЯвЛЕуЃЌСЌDEЃЌЙ§ЕуDзїDFDEЧвDF DE ЃЌСЌCF НЛ DO ЕФбгГЄЯпгкЕуG ШєOG 4ЃЌЧѓCE ЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉCE=OT=8ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩOCЁЭODЃЌCAЁЭBDжЊЁЯCOD=ЁЯBCA=ЁЯAOB=90ЁуЃЌДгЖјЕУЁЯAOC=ЁЯBODЃЌЁЯOBD=ЁЯOACЃЌНсКЯOC=ODжЄЁїAOCЁеЁїBODПЩЕУД№АИЃЛ
ЃЈ2ЃЉзїANЁЮODЃЌНЛOMбгГЄЯпгкЕуNЃЌЯШжЄЁїBOCЁеЁїOANЕУBC=ONЃЌAN=OC=ODЃЌдйжЄЁїAMNЁеЁїDMOЕУOM=MN=![]() ONЃЌДгЖјЕУжЄЃЛ
ONЃЌДгЖјЕУжЄЃЛ
ЃЈ3ЃЉзїFTЁЭDGЃЌНЛDGбгГЄЯпгкЕуTЃЌЯШжЄЁїFTDЁеЁїDOEЕУFT=OD=OCЃЌDT=OEЃЌдйжЄЁїFTGЁеЁїCOGЕУOT=2OG=8ЃЌИљОнOE=DTЃЌOC=ODПЩЕУCE=OTЃЎ
НтЃКЃЈ1ЃЉЁпOCЁЭODЃЌCAЁЭBDЃЌ
ЁрЁЯCOD=ЁЯBCA=ЁЯAOB=90ЁуЃЌ
ЁрЁЯBOC+ЁЯCOE=90Ёу, ЁЯDOE+ЁЯCOE=90Ёу,
ЁрЁЯBOC=ЁЯDOE,
ЁрЁЯAOC=ЁЯBODЃЌ
ЭЌРэПЩжЄЁЯOBD=ЁЯOACЃЌ
дкЁїAOCКЭЁїBODжаЃЌ
Ёп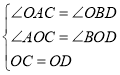 ЃЌ
ЃЌ
ЁрЁїAOCЁеЁїBODЃЈAASЃЉЃЌ
ЁрOA=OBЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуAзїANЁЮODЃЌНЛOMбгГЄЯпгкЕуNЃЌ

дђЁЯOAN+ЁЯAOD=180ЁуЃЌ
ЁпЁЯAOB=ЁЯCOD=90ЁуЃЌ
ЁрЁЯAOD+ЁЯBOC=180ЁуЃЌ
ЁрЁЯOAN=ЁЯBOCЃЌ
гжЁпOMЁЮACЃЌ
ЁрЁЯAON=ЁЯCAOЃЌ
гЩЃЈ1ЃЉжЊЁЯCAO=ЁЯOBCЃЌ
ЁрЁЯAON=ЁЯOBCЃЌ
гжЁпOA=OBЃЌ
ЁрЁїBOCЁеЁїOANЃЈASAЃЉЃЌ
ЁрBC=ONЃЌAN=OC=ODЃЌ
ЁпANЁЮODЃЌ
ЁрЁЯMAN=ЁЯMDOЃЌЁЯMNA=ЁЯMODЃЌ
ЁрЁїAMNЁеЁїDMOЃЈASAЃЉЃЌ
ЁрOM=MN=![]() ONЃЌМДON=2OMЃЌ
ONЃЌМДON=2OMЃЌ
ЁрBC=2OMЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуFзїFTЁЭDGЃЌНЛDGбгГЄЯпгкЕуTЃЌ
дђЁЯFTD=ЁЯDOE=90ЁуЃЌ
ЁрЁЯODE+ЁЯOED=90ЁуЃЌ
гжЁпDEЁЭDFЃЌ
ЁрЁЯODE+ЁЯFDT=90ЁуЃЌ
ЁрЁЯOED=ЁЯTDFЃЌ
ЁпDE=DFЃЌ
ЁрЁїFTDЁеЁїDOEЃЈAASЃЉЃЌ
ЁрFT=ODЃЌDT=OEЃЌ
ЁпOD=OCЃЌ
ЁрFT=OCЃЌ
ЁпЁЯFTG=ЁЯCOG=90ЁуЃЌЁЯFGT=ЁЯCGOЃЌ
ЁрЁїFTGЁеЁїCOGЃЈAASЃЉЃЌ
ЁрOT=2OG=8ЃЌ
ЁпOE=DTЃЌOC=ODЃЌ
ЁрCE=OT=8ЃЎ


 Н№ХЦНЬИЈХргХгХбЁОэЦкФЉГхДЬ100ЗжЯЕСаД№АИ
Н№ХЦНЬИЈХргХгХбЁОэЦкФЉГхДЬ100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯABC=ЁЯADC=90ЁуЃЌСЌНгACЁЂBDЃЌMЁЂNЗжБ№ЪЧACЁЂBDЕФжаЕуЃЌСЌНгMN
(1)ЧѓжЄЃКMNЁЭBD.
(2)ШєЁЯDAC=62ЁуЃЌЁЯBAC=58ЁуЃЌЧѓЁЯDMB

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭЈЙ§ЖдЯТУцЪ§бЇФЃаЭЕФбаОПбЇЯАЃЌНтОіЯТСаЮЪЬтЃК
ЃЈФЃаЭГЪЯжЃЉ
(1)ШчЭМ1ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() .гЩ
.гЩ![]() ЃЌЕУ
ЃЌЕУ![]() .гж
.гж![]() ЃЌПЩвдЭЦРэЕУЕН
ЃЌПЩвдЭЦРэЕУЕН![]() .НјЖјЕУЕН
.НјЖјЕУЕН![]() _____ЃЌ
_____ЃЌ![]() _____.ЮвУЧАбетИіЪ§бЇФЃаЭГЦЮЊЁА
_____.ЮвУЧАбетИіЪ§бЇФЃаЭГЦЮЊЁА![]() зжЁБФЃаЭЛђЁАвЛЯпШ§ЕШНЧЁБФЃаЭЃЛ
зжЁБФЃаЭЛђЁАвЛЯпШ§ЕШНЧЁБФЃаЭЃЛ
ЃЈФЃаЭгІгУЃЉ
(2)ЂйШчЭМ2ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гыжБЯп
гыжБЯп![]() НЛгкЕу
НЛгкЕу![]() .ЧѓжЄЃКЕу
.ЧѓжЄЃКЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕу.
ЕФжаЕу.
ЂкШчЭМ3ЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЮЊЦНУцФкШЮвЛЕуЃЌЕу
ЮЊЦНУцФкШЮвЛЕуЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() .Шє
.Шє![]() ЪЧвд
ЪЧвд![]() ЮЊаББпЕФЕШбќжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕу
ЮЊаББпЕФЕШбќжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕу![]() ЕФзјБъ.
ЕФзјБъ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪЕбщжабЇЮЊСЫНтбЇЩњЁАзюЪЪКЯздМКЕФПМЧАМѕбЙЗНЪНЁБЃЌдкОХФъМЖЗЖЮЇФкПЊеЙСЫвЛДЮГщбљЕїВщЃЌбЇЩњБиаыдкЫФРрбЁЯюжабЁдёвЛЯюЃЌаЁУїИљОнЕїВщНсЙћЛцжЦСЫШчЯТЩаВЛЭъећЕФЭГМЦЭМЃЎ
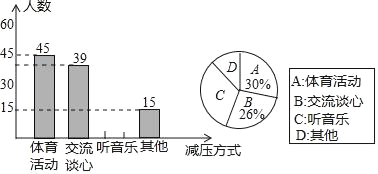
ЧыИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉетДЮГщбљЕїВщжаЃЌГщВщЕФбЇЩњШЫЪ§ЮЊ______ШЫЃЎ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ3ЃЉЩШаЮЭГМЦЭМжаЁАЦфЫћЁБЫљЖдгІЩШаЮдВаФНЧЮЊ______ЖШЃЎ
ЃЈ4ЃЉШєЪЕбщжабЇОХФъМЖга700ШЫЃЌЧыЙРМЦВЩгУЁАЬ§вєРжЁБзїЮЊМѕбЙЗНЪНЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЖЈФмШЗЖЈЁїABCЁеЁїDEFЕФЬѕМўЪЧЃЈ ЃЉ
A.AB=DE,BC=EF,ЁЯA=ЁЯDB.ЁЯA=ЁЯE,AB=EF,ЁЯB=ЁЯD
C.ЁЯA=ЁЯD,AB=DE,ЁЯB=ЁЯED.ЁЯA=ЁЯD,ЁЯB=ЁЯE,ЁЯC=ЁЯF
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
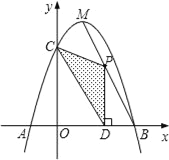
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љx2+bx+cгыxжсЯрНЛгкAЁЂBСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌЧвЕуBгыЕуCЕФзјБъЗжБ№ЮЊBЃЈ3ЃЌ0ЃЉЃЎCЃЈ0ЃЌ3ЃЉЃЌЕуMЪЧХзЮяЯпЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕуPЮЊЯпЖЮMBЩЯвЛИіЖЏЕуЃЌЙ§ЕуPзїPDЁЭxжсгкЕуDЃЎШєOD=mЃЌЁїPCDЕФУцЛ§ЮЊSЃЌЪдХаЖЯSгазюДѓжЕЛђзюаЁжЕЃПВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкMBЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїPCDЮЊжБНЧШ§НЧаЮЃПШчЙћДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮ ABCD жаЃЌAB=8ЃЌBC=6ЃЌНЋОиаЮ ABCD ШЦЕу A ФцЪБеыа§зЊЕУЕНОиаЮ AEFGЃЌAEЃЌFG ЗжБ№НЛЩфЯпCD гкЕу PHЃЌСЌНс AHЃЌШє P ЪЧ CH ЕФжаЕуЃЌдђЁїAPH ЕФжмГЄЮЊЃЈ ЃЉ
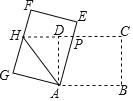
A. 15 B. 18 C. 20 D. 24
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП (1)дФЖСРэНт:
ЮвУЧжЊЕРЃЌжЛгУжБГпКЭдВЙцВЛФмНтОіЕФШ§ИіОЕфЕФЯЃРАЮЪЬтжЎвЛЪЧШ§ЕШЗжШЮвтНЧЃЌЕЋЪЧетИіШЮЮёПЩвдНшжњШчЭМЫљЪОЕФвЛБпЩЯгаПЬЖШЕФЙДГпЭъГЩЃЌЙДГпЕФжБНЧЖЅЕуЮЊPЃЌЁАПэБлЁБЕФПэЖШ=PQ= QR = RS,(етИіЬѕМўКмживЊХЖЃЁ)ЙД ГпЕФвЛБп MN ТњзуM, N, QШ§ЕуЙВЯп(ЫљвдPQ ЁЭ MN).
ЯТУцвдШ§ЕШЗжЁЯABCЮЊР§ЫЕУїРћгУЙДГпШ§ЕШЗжШёНЧЕФЙ§ГЬ:
ЕквЛВН:ЛжБЯпDEЪЙDE //BCЃЌЧветСНЬѕЦНааЯпЕФОрРыЕШгкPQ;
ЕкЖўВН:вЦЖЏЙДГпЕНКЯЪЪЮЛжУЃЌЪЙЦфЖЅЕуPТфдкDEЩЯЃЌЪЙЙДГпЕФMNБпОЙ§ЕуBЃЌЭЌЪБШУЕуRТфдкЁЯABCЕФBAБпЩЯ;
ЕкШ§ВН:БъМЧДЫЪБЕуQКЭЕуPЫљдкЮЛжУЃЌзїЩфЯпBQКЭЩфЯпBP:
ЧыЭъГЩЕкШ§ВНВйзїЃЌЭМжаЁЯABCЕФШ§ЕШЗжЯпЪЧЩфЯп ЁЂ .
ЃЈ2ЃЉдк(1)ЕФЬѕМўЯТВЙШЋШ§ЕШЗжЁЯABCЕФжївЊжЄУїЙ§ГЬ:
Ёп ЃЌBQ ЁЭ PRЃЌ
ЁрBP= BR.ЃЈЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕугыетЬѕЯпЖЮСНИіЖЫЕуЕФОрРыЯрЕШЃЉ
ЁрЁЯRBQ=ЁЯPBQЃЌ
ЁпPTЁЭBCЃЌPQЁЭBQЃЌPT=PQЃЌ
ЁрЁЯ = ЁЯ . ЃЈНЧЕФФкВПЕННЧЕФСНБпОрРыЯрЕШЕФЕудкНЧЕФЦНЗжЯпЩЯЃЉ
ЁрЁЯ = = ЁЯ = ЁЯ
ЃЈ3ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЬНОПЃК
ЁЯABS=![]() ЁЯABCЪЧЗёГЩСЂЃПШчЙћГЩСЂЃЌЧыЫЕУїРэгЩЃЛШчЙћВЛГЩСЂЃЌЧыдкЯТЭМжаЁЯABCЭтВПЛГіЁЯABV =
ЁЯABCЪЧЗёГЩСЂЃПШчЙћГЩСЂЃЌЧыЫЕУїРэгЩЃЛШчЙћВЛГЩСЂЃЌЧыдкЯТЭМжаЁЯABCЭтВПЛГіЁЯABV =![]() ЁЯABCЃЈЮоашаДЛЗЈЃЌБЃСєЛЭМКлМЃМДПЩЃЉ
ЁЯABCЃЈЮоашаДЛЗЈЃЌБЃСєЛЭМКлМЃМДПЩЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
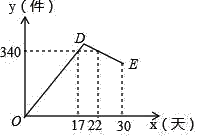
ЁОЬтФПЁПФГЙЋЫОПЊЗЂГівЛПюаТЕФНкФмВњЦЗЃЌИУВњЦЗЕФГЩБОМлЮЊ6дЊМўЃЌИУВњЦЗдке§ЪНЭЖЗХЪаГЁЧАЭЈЙ§ДњЯњЕуНјааСЫЮЊЦк30ЬьЕФЪдЯњЪлЃЌЪлМлЮЊ8дЊ/МўЃЌЙЄзїШЫдБЖдЯњЪлЧщПіНјааСЫИњзйМЧТМЃЌВЂНЋМЧТМЧщПіЛцГЩШчЭМЫљЪОЕФЭМЯѓЃЌЭМжаЕФелЯпODEБэЪОШеЯњЪлСПyЃЈМўЃЉгыЯњЪлЪБМфxЃЈЬьЃЉжЎМфЕФКЏЪ§ЙиЯЕЃЌвбжЊЯпЖЮDEБэЪОЕФКЏЪ§ЙиЯЕжаЃЌЪБМфУПдіМг1ЬьЃЌШеЯњЪлСПМѕЩй5МўЃЎ
ЃЈ1ЃЉЕк24ЬьЕФШеЯњЪлСПЪЧЁЁ ЁЁМўЃЌШеЯњЪлРћШѓЪЧЁЁ ЁЁдЊЃЎ
ЃЈ2ЃЉЧѓЯпЖЮDEЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЃЎЃЈВЛвЊЧѓаДГіздБфСПЕФШЁжЕЗЖЮЇЃЉ
ЃЈ3ЃЉЭЈЙ§МЦЫуЫЕУїЪдЯњЪлЦкМфЕкМИЬьЕФШеЯњЪлСПзюДѓЃПзюДѓШеЯњЪлСПЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com