
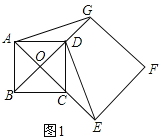
【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点![]() 到点E,使
到点E,使![]() ,然后以OG、OE为邻边作正方形OEFG,连接
,然后以OG、OE为邻边作正方形OEFG,连接![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 正方形ABCD固定,将正方形OEFG绕点O逆时针旋转
正方形ABCD固定,将正方形OEFG绕点O逆时针旋转![]() 角
角![]() 得到正方形
得到正方形![]() ,如图2.
,如图2.
![]() 在旋转过程中,当
在旋转过程中,当![]() 是直角时,求
是直角时,求![]() 的度数;
的度数;
![]() 若正方形ABCD的边长为1,在旋转过程中,求
若正方形ABCD的边长为1,在旋转过程中,求![]() 长的最大值和此时
长的最大值和此时![]() 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.

【答案】(1)见解析;(2)![]() ;
;![]()
【答题空27-1】![]()
【答题空27-2】![]()
【解析】分析:(1)延长ED交AG于点H,证明![]() ≌
≌![]() ,根据等量代换证明结论;
,根据等量代换证明结论;
(2)根据题意和锐角正弦的概念以及特殊角的三角函数值得到![]() ,分两种情况求出
,分两种情况求出![]() 的度数;
的度数;
(3)根据正方形的性质分别求出OA和OF的长,根据旋转变换的性质求出AF′长的最大值和此时![]() 的度数.
的度数.
详解:![]() 如图1,延长ED交AG于点H,
如图1,延长ED交AG于点H,
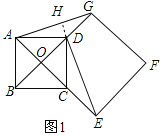
![]() 点O是正方形ABCD两对角线的交点,
点O是正方形ABCD两对角线的交点,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
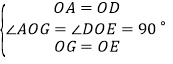 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ;
;
![]() 在旋转过程中,
在旋转过程中,![]() 成为直角有两种情况:
成为直角有两种情况:
![]() Ⅰ
Ⅰ![]() 由
由![]() 增大到
增大到![]() 过程中,当
过程中,当![]() 时,
时,
![]() ,
,
![]() 在
在![]() 中,sin∠AGO=
中,sin∠AGO=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ;
;
![]() Ⅱ
Ⅱ![]() 由
由![]() 增大到
增大到![]() 过程中,当
过程中,当![]() 时,
时,
同理可求![]() ,
,
![]() .
.
综上所述,当![]() 时,
时,![]() 或
或![]() .
.
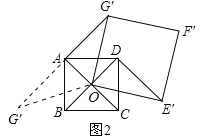
![]() 如图3,
如图3,
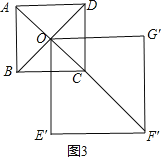
当旋转到A、O、![]() 在一条直线上时,
在一条直线上时,![]() 的长最大,
的长最大,
![]() 正方形ABCD的边长为1,
正方形ABCD的边长为1,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 此时
此时![]() .
.


科目:初中数学 来源: 题型:
【题目】分别观察下面的左、右两组等式:


根据你发现的规律解决下列问题:
(1)填空:________![]() ;
;
(2)已知![]() ,则x的值是________;
,则x的值是________;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是数轴上表示-2与-1两数的点为端点的线段的中点.
![]()
(1)数轴上点P表示的数为 ;
(2)在数轴上距离点P为2.5个单位长度的点表示的数为 ;
(3)如图,若点P是线段AB(点A在点B的左侧)的中点,且点A表示的数为m,那么点B表示的数是 .(用含m的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
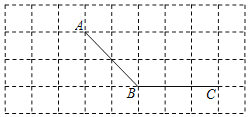
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
![]() 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;
![]() 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E;
![]() 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;
![]() 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;
![]() 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______![]() 用“
用“![]() ”连接
”连接![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.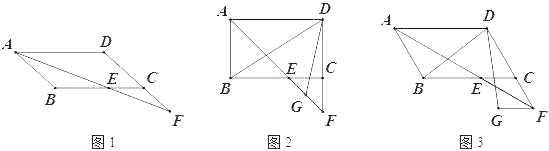
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字﹣3,1,3的不透明卡片,它们除数字外都相同,现将它们背面朝上,洗匀后从三张卡片中随机地抽取一张,放回卡片洗匀后,再从三张卡片中随机地抽取一张.
(1)试用列表或画树状图的方法,求两次抽取的卡片上的数字之积为负数的概率;
(2)求两次抽取的卡片上的数字之和为非负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某装修公司为某新建小区的A、B两种户型(共300套)装修地板
(1)若A种户型所需木地板、地板砖各为50m2、20m2,B种户型所需木地板、地板砖各为40m2、25m2.公司最多可提供木地板13000m2,最多可提供地板砖7010m2,在此条件下,则可能装修A、B两种户型各多少套?
(2)小王在该小区购买了一套A户型套房(地面总面积为70m2).现有两种铺设地面的方案:①卧室铺实木地板,卧室以外铺亚光地板砖;②卧室铺强化木地板,卧室以外铺抛光地板砖.经预算,铺1m2地板的平均费用如下表.设卧室地面面积为am2,怎样选择所需费用更低?
类别 | 抛光地板砖 | 亚光地板砖 | 实木地板 | 强化木地板 |
平均费用(元/m2) | 170 | 90 | 200 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查作业:了解你所住小区家庭5月份用气量情况.
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2-5之间,这300户家庭的平均人数均为3.4.
小天、小东、小芸各自对该小区家庭5月份用气量情况进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1 抽样调查小区4户家庭5月份用气量统计表 (单位:![]() )
)

表2 抽样调查小区15户家庭5月份用气量统计表 (单位:![]() )
)

表3 抽样调查小区15户家庭5月份用气量统计表 (单位:![]() )
)

根据以上材料回答问题:
小天、小东和小芸三人中,哪一位同学抽样调查的数据能较好地反映出该小区家庭5月份用气量情况,并简要说明其他两位同学抽样调查地不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
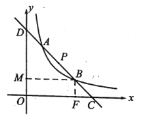
【题目】已知直线l过点P(2, 2),且与函数y=![]() (x>0)的图象相交于A, B两点,与x轴、y轴分别交于点C, D,如图所示,四边形OFBM为矩形,面积为3.
(x>0)的图象相交于A, B两点,与x轴、y轴分别交于点C, D,如图所示,四边形OFBM为矩形,面积为3.
(1)求k的值;
(2)当点B的横坐标为3时,求直线l的解析式及线段BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com