练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，在平面直角坐标系中，抛物线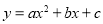经过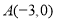、、三点，其顶点为D，连接AD，点P是线段AD上一个动点（不与A、D重合）．经过点P作y轴的垂线，重足为E，连接AE．

    （1）求抛物线的函数解析式，并写出顶点D的坐标；

    （2）如果P点的坐标为（x,y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量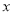的取值范围，并求S的最大值；

    （3）在（2）的条件下，当S取到最大值时，过点P作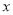轴的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为点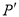，求出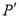的坐标，并判断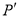是否在该抛物线上．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014-2015学年山东省龙口市五中初中毕业班下学期期中考试数学试卷（解析版） 题型：填空题

    已知分式方程产生增根，则m的值为___________．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年内蒙古满洲里市九年级4月月考数学试卷（解析版） 题型：选择题

    在-3．5，，0，，,,0．161161116中，无理数有（ ）个

    A、1 B、2 C、3 D、4

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年江苏省九年级下学期3月月考数学试卷（解析版） 题型：填空题

    一只蜜蜂将随意落在如图的方格中，每个小方格形状完全相同，则蜜蜂落在阴影部分的概率是 ．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年江苏省九年级下学期3月月考数学试卷（解析版） 题型：选择题

    如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，已知AE=9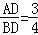，，则EC的长是（ ）

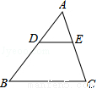
    A．4．5 B．8 C．12 D．14

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年广东省惠阳区三中初中毕业生学业综合测试数学试卷（解析版） 题型：解答题

    某汽车运输公司根据实际需要计划购买大、中型两种客车共20辆，已知大型客车每辆62万元，中型客车每辆40万元，设购买大型客车x（辆），购车总费用为y（万元）．

    （1）求y与x的函数关系式（不要求写出自变量x的取值范围）；

    （2）若购买中型客车的数量少于大型客车的数量，请你给出一种费用最省的方案，并求出该方案所需费用．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年广东省惠阳区三中初中毕业生学业综合测试数学试卷（解析版） 题型：填空题

    二次函数的最小值是 ．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年广东省广州市番禺区综合测试（一模）数学试卷（解析版） 题型：解答题

    （本小题满分12分）如图，在平面直角坐标系xOy中，若点A（－2，n），B（1，－2）是一次函数y=kx+b的图象和反比例函数y=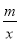的图象的两个交点．

    （1）求反比例函数和一次函数的解析式；

    （2）求直线AB与x轴的交点C的坐标；

    （3）求点到直线AB的距离．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年广东省高要市中考一模数学试卷（解析版） 题型：选择题

    下列运算正确的是（ ）

    A． B．=

    C．=3 D．

    查看答案和解析>>

    同步练习册答案