
【题目】如图,![]() 是一张直角三角形彩色纸,
是一张直角三角形彩色纸,![]() ,
,![]() 30
30![]() ,
,![]() 40
40![]() ,
,![]() 于点
于点![]() .将斜边上的高
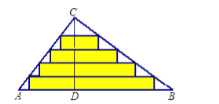
.将斜边上的高![]() 进行五等分,然后裁出4张宽度相等的长方形纸条.则这4张纸条的面积和是______
进行五等分,然后裁出4张宽度相等的长方形纸条.则这4张纸条的面积和是______![]() .
.
【答案】480
【解析】
先利用勾股定理计算出AB=50cm,再利用面积法可计算出CD=24cm,证明△CEF∽△CAB,由于斜边上的高CD被五等分,所以![]() 则EF=
则EF=![]() ×50=10,同理可得MN=
×50=10,同理可得MN=![]() AB=20,PQ=
AB=20,PQ=![]() AB=30,GH=
AB=30,GH=![]() AB=40,然后根据矩形的面积公式计算.
AB=40,然后根据矩形的面积公式计算.
∵∠ACB=90![]() ,AC=30cm,BC=40cm,
,AC=30cm,BC=40cm,
∴AB=![]() =50(cm),
=50(cm),
∵![]() CDAB=
CDAB=![]() ACBC,
ACBC,
∴CD=![]() =24(cm),CK=
=24(cm),CK=![]() (cm)
(cm)
如图,∵EF∥AB,
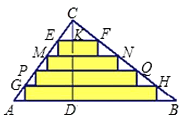
∴△CEF∽△CAB,
∴![]() ,
,
∴EF=![]() ×50=10,
×50=10,
同样方法可得MN=![]() AB=20,
AB=20,
PQ=![]() AB=30,
AB=30,
GH=![]() AB=40,
AB=40,
∴这4张纸条的面积和=10×![]() +20×
+20×![]() +30×
+30×![]() +40×
+40×![]()
故答案:480.


科目:初中数学 来源: 题型:
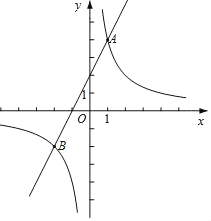
【题目】如图,在平面直角坐标系xOy中,直线y=2x+2与函数y=![]() (k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(1)求k,m的值;
(2)已知点P(a,0),过点P作平行于y轴的直线,交直线y=2x+2于点M,交函数y=![]() (k≠)的图象于点N.
(k≠)的图象于点N.
①当a=2时,求线段MN的长;
②若PM>PN,结合函数的图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
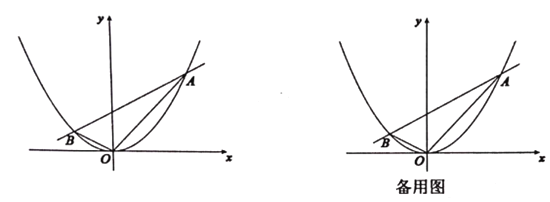
【题目】如图所示,抛物线![]() 与直线
与直线![]() 交于两点
交于两点![]() .已知点
.已知点![]() 坐标为
坐标为![]()
(1)求![]() 点坐标;
点坐标;
(2)求![]() 的面积;
的面积;
(3)将直线![]() 从原点出发向上平移
从原点出发向上平移![]() 个单位,设
个单位,设![]() 为直线平移后其上一点,且满足
为直线平移后其上一点,且满足![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
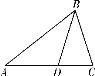
【题目】如图,在△ABC中,BD是△ABC的角平分线.
(1)尺规作图:作BD的垂直平分线分别交AB,BC于点M,N;(保留作图痕迹,不写作法)
(2)连接MD,ND,判断四边形BMDN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中
中![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,作
,作![]() 与
与![]() 相切于点
相切于点![]() ,在
,在![]() 边上取一点
边上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
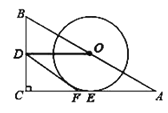
(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() ,
,![]() 时,求
时,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程![]() ,
,![]() ,其中
,其中![]() ,下列四个结论中,错误的是( )
,下列四个结论中,错误的是( )
A. 如果方程![]() 有两个不相等的实数根,那么方程
有两个不相等的实数根,那么方程![]() 也有两个不相等的实数根
也有两个不相等的实数根
B. ![]() 时,方程
时,方程![]() 和方程
和方程![]() 有一个相同的根,那么这个根必是
有一个相同的根,那么这个根必是![]()
C. 如果![]() 是方程
是方程![]() 的一个根,那么
的一个根,那么![]() 是方程
是方程![]() 的一个根
的一个根
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
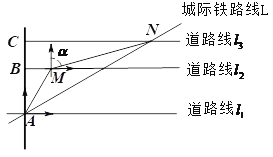
【题目】下图为某区域部分交通线路图,其中直线![]() ,直线
,直线![]() 与直线
与直线![]() 都垂直,,垂足分别为点A、点B和点C,(高速路右侧边缘),
都垂直,,垂足分别为点A、点B和点C,(高速路右侧边缘),![]() 上的点M位于点A的北偏东30°方向上,且BM=
上的点M位于点A的北偏东30°方向上,且BM=![]() 千米,
千米,![]() 上的点N位于点M的北偏东
上的点N位于点M的北偏东![]() 方向上,且
方向上,且![]() ,MN=
,MN=![]() 千米,点A和点N是城际线L上的两个相邻的站点.
千米,点A和点N是城际线L上的两个相邻的站点.
(1)求![]() 之间的距离
之间的距离
(2)若城际火车平均时速为150千米/小时,求市民小强乘坐城际火车从站点A到站点N需要多少小时?(结果用分数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.
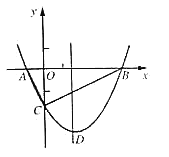
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是抛物线对称轴上的一个动点,当
是抛物线对称轴上的一个动点,当![]() 周长最小时,求点
周长最小时,求点![]() 的坐标及
的坐标及![]() 的最小周长.
的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2)延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x 轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2018个正方形的面积为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com