
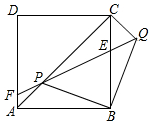
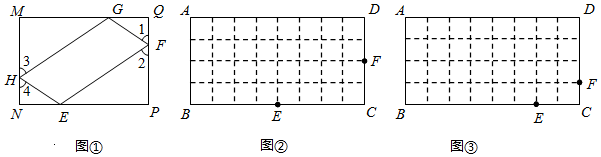
 边长为2$\sqrt{2}$的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
边长为2$\sqrt{2}$的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.分析 (1)证出∠ABP=∠CBQ,由SAS证明△BAP≌△BCQ可得结论;
(2)如图1证明△APB∽△CEP,列比例式可得y与x的关系式,根据CE=$\frac{3}{8}$BC计算CE的长,即y的长,代入关系式解方程可得x的值;
(3)如图3,作辅助线,构建全等三角形,证明△PGB≌△QEB,得EQ=PG,由F、A、G、P四点共圆,
得∠FGP=∠FAP=45°,所以△FPG是等腰直角三角形,可得结论.
如图4,当F在AD的延长线上时,同理可得结论.
解答 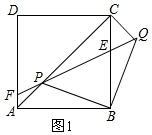 (1)证明:如图1,∵线段BP绕点B顺时针旋转90°得到线段BQ,
(1)证明:如图1,∵线段BP绕点B顺时针旋转90°得到线段BQ,
∴BP=BQ,∠PBQ=90°.
∵四边形ABCD是正方形,
∴BA=BC,∠ABC=90°.
∴∠ABC=∠PBQ.
∴∠ABC-∠PBC=∠PBQ-∠PBC,即∠ABP=∠CBQ.
在△BAP和△BCQ中,
∵$\left\{\begin{array}{l}{BA=BC}\\{∠ABP=∠CBQ}\\{BP=BQ}\end{array}\right.$,
∴△BAP≌△BCQ(SAS).
∴CQ=AP;
(2)解:如图1,∵四边形ABCD是正方形,
∴∠BAC=$\frac{1}{2}$∠BAD=45°,∠BCA=$\frac{1}{2}$∠BCD=45°,
∴∠APB+∠ABP=180°-45°=135°,
∵DC=AD=2$\sqrt{2}$,
由勾股定理得:AC=$\sqrt{(2\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=4,
∵AP=x,
∴PC=4-x,
∵△PBQ是等腰直角三角形,
∴∠BPQ=45°,
∴∠APB+∠CPQ=180°-45°=135°,
∴∠CPQ=∠ABP,
∵∠BAC=∠ACB=45°,
∴△APB∽△CEP,
∴$\frac{AP}{CE}=\frac{AB}{CP}$,
∴$\frac{x}{y}=\frac{2\sqrt{2}}{4-x}$,
∴y=$\frac{1}{2\sqrt{2}}$x(4-x)=-$\frac{\sqrt{2}}{4}{x}^{2}+\sqrt{2}$x(0<x<4),
由CE=$\frac{3}{8}$BC=$\frac{3}{8}×2\sqrt{2}$=$\frac{3\sqrt{2}}{4}$,
∴y=-$\frac{\sqrt{2}}{4}{x}^{2}+\sqrt{2}$x=$\frac{3\sqrt{2}}{4}$,
x2-4x+3=0,
(x-3)(x-1)=0,
x=3或1,
∴当x=3或1时,CE=$\frac{3}{8}$BC;
(3)解:结论:PF=EQ,理由是:
如图2,当F在边AD上时,过P作PG⊥FQ,交AB于G,则∠GPF=90°,
∵∠BPQ=45°,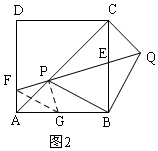
∴∠GPB=45°,
∴∠GPB=∠PQB=45°,
∵PB=BQ,∠ABP=∠CBQ,
∴△PGB≌△QEB,
∴EQ=PG,
∵∠BAD=90°,
∴F、A、G、P四点共圆,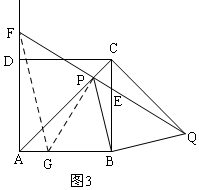
连接FG,
∴∠FGP=∠FAP=45°,
∴△FPG是等腰直角三角形,
∴PF=PG,
∴PF=EQ.
当F在AD的延长线上时,如图3,同理可得:PF=PG=EQ.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、勾股定理、四点共圆的性质和判定、相似三角形的判定与性质等知识;本题综合性强,有一定难度.


科目:初中数学 来源: 题型:选择题
| A. | y<0 | B. | 0<y<m | C. | m<y<m+4 | D. | y>m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=8,AB=5,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=8,AB=5,则AE的长为( )| A. | 5 | B. | 6 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
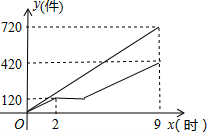 甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.
甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com