
【题目】如图,E是边长为1的正方形ABCD的对角线BD上一动点,点E从点B向点D运动(与点B,D不重合),过点E作直线GH∥BC,交AB于点G,交CD于点H,EF⊥AE,交CD(或CD的延长线)于点F.
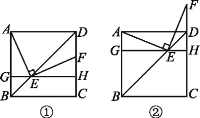
(1)如图①,求证:△AGE≌△EHF.
(2)在点E的运动过程中(如图①,②),四边形AFHG的面积是否会发生变化?请说明理由.
【答案】(1)见解析;(2)四边形AFHG的面积不会发生变化,都是![]() ;理由见解析.
;理由见解析.
【解析】
(1)根据四边形ABCD是正方形,BD是对角线,且GH∥BC可证明AGHD是矩形,∠AGE=∠EHF=90°,AG=DH,△GBE是等腰直角三角形,可得DH=HE,即可证明AG=EH,利用EF⊥AE及直角三角形两锐角互余的关系可得∠AEG=∠EFH,根据AAS即可证明△AGE≌△EHF;
(2)分两种情况进行讨论:①当点E运动到BD的中点时,可得四边形AFHG是矩形,可得S四边形AFHG=![]() ;②当点E不在BD的中点时,点E在运动(与点B、D不重合)的过程中,四边形AFHG是直角梯形,由(1)知,△AGE≌△EHF,图②时,同(1)的证明方法可得△AGE≌△EHF,S四边形AFHG=
;②当点E不在BD的中点时,点E在运动(与点B、D不重合)的过程中,四边形AFHG是直角梯形,由(1)知,△AGE≌△EHF,图②时,同(1)的证明方法可得△AGE≌△EHF,S四边形AFHG=![]() (FH+AG)GH=
(FH+AG)GH=![]() ,然后即可得出结论.
,然后即可得出结论.
(1)∵四边形ABCD是正方形,GH∥BC,
∴AGHD是矩形,
∴∠AGE=∠EHF=90°,AG=DH,
∵BD是对角线,
∴∠HDE=45°,
∴△EHD是等腰直角三角形,
∴DH=HE,
∴AG=EH.
∵EF⊥AE,
∴∠AEG+∠FEH=90°.
∵∠EFH+∠FEH=90°,
∴∠AEG=∠EFH.
在△AGE和△EHF中,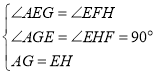 ,
,
∴△AGE≌△EHF(AAS).
(2)四边形AFHG的面积不会发生变化.
理由:①当E运动到BD的中点时,F与D重合,
∴四边形AFHG是矩形,
∵E为BD中点,GH//BC,
∴DH=![]() CD=
CD=![]() ,
,
∴S四边形AFHG=![]() ,
,
②当E不在BD的中点时,在点E的运动(与点B、D不重合)过程中,四边形AFHG是直角梯形.
由(1)知图①中△AGE≌△EHF,
如图②,∵ABCD是正方形,GH//BC,
∴AGHD是矩形,
∴AG=HD,∠AGE=∠EHF=90°,
∵E在对角线BD上,
∴∠EDH=45°,
∴△EDH是等腰直角三角形,
∴EH=HD,
∴AG=EH,
∵EF⊥AE,
∴∠AEG+∠FEH=90°,
∵∠F+∠FEH=90°,
∴∠AEG=∠F,
在△AGE和△EHF中,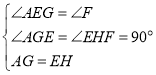 ,
,
∴△AGE≌△EHF(AAS).
∴FH=EG=BG,
∴FH+AG=BG+AG=AB=1.
∴S四边形AFHG=![]() (FH+AG)·GH=
(FH+AG)·GH=![]() .
.
综上所述,四边形AFHG的面积不会发生变化,都是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校组织学生开展为贫困山区孩子捐书活动,要求捐赠的书籍类别为科普类、文学类、漫画类、哲学故事类、环保类,学校图书管理员对所捐赠的书籍随机抽查了部分进行统计,并对获取的数据进行了整理,根据整理结果,绘制了如图所示的两幅不完整的统计图.已知所统计的数据中,捐赠的哲学故事类书籍和文学类书籍的数量相同.请根据以上信息,解答下列问题:

(1)本次被抽查的书籍有_____册.
(2)补全条形统计图.
(3)若此次捐赠的书籍共1200册,请你估计所捐赠的科普类书籍有多少册.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB的长为10,弦AC长为6,∠ACB的平分线交⊙O于D.
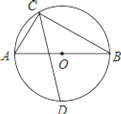
(1)求BC的长.
(2)连接AD和BD,判断△ABD的形状,说明理由.并求BD的长.
(3)求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:O上两个定点A,B和两个动点C,D,AC与BD交于点E.
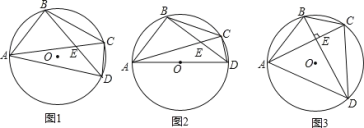
(1)如图1,求证:EAEC=EBED;
(2)如图2,若AB=BC,AD是O的直径,求证:ADAC=2BDBC;
(3) 如图3,若AC⊥BD,点O到AD的距离为2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
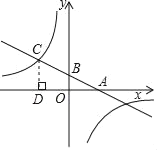
【题目】如图,已知一次函数y=ax+b(a,b为常数,a≠0)的图象与x轴,y轴分别交于点A,B,且与反比例函数y=![]() (k为常数,k≠0)的图象在第二象限内交于点C,作CD⊥x轴于,若OA=OD=
(k为常数,k≠0)的图象在第二象限内交于点C,作CD⊥x轴于,若OA=OD=![]() OB=3.
OB=3.
(1)求一次函数与反比例函数的解析式;
(2)观察图象直接写出不等式0<ax+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材在墙中,不知其大小用锯子去锯这个木材,锯口深DE=1寸,锯道长AB=10寸,问这块圆形木材的直径是多少?”
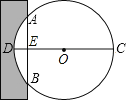
查看答案和解析>>
科目:初中数学 来源: 题型:
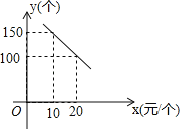
【题目】某旅游风景区出售一种纪念品,该纪念品的成本为![]() 元/个,这种纪念品的销售价格为
元/个,这种纪念品的销售价格为![]() (元/个)与每天的销售数量
(元/个)与每天的销售数量![]() (个)之间的函数关系如图所示.
(个)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)销售价格定为多少时,每天可以获得最大利润?并求出最大利润.
(3)“十一”期间,游客数量大幅增加,若按八折促销该纪念品,预计每天的销售数量可增加![]() ,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习与圆有关的角时了解到:在同圆或等圆中,同弧(或等弧)所对的圆周角相等.如图,点A、B、C、D均为⊙O上的点,则有∠C=∠D.
小明还发现,若点E在⊙O外,且与点D在直线AB同侧,则有∠D >∠E. 请你参考小明得出的结论,解答下列问题:
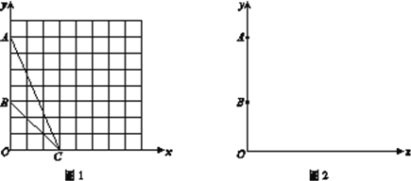
(1)如图1,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0) .①在图1中作出△ABC的外接圆(保留必要的作图痕迹,不写作法);
②若在![]() 轴的正半轴上有一点D,且∠ACB =∠ADB,则点D的坐标为________;
轴的正半轴上有一点D,且∠ACB =∠ADB,则点D的坐标为________;
(2) 如图2,在平面直角坐标系xOy中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0.点P为![]() 轴正半轴上的一个动点,当∠APB达到最大时,直接写出此时点P的坐标.
轴正半轴上的一个动点,当∠APB达到最大时,直接写出此时点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com