
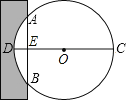
【题目】《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材在墙中,不知其大小用锯子去锯这个木材,锯口深DE=1寸,锯道长AB=10寸,问这块圆形木材的直径是多少?”
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,用同样规格黑白两色的正方形瓷砖铺设长方形地面,请观察下列图形,并解答有关问题:
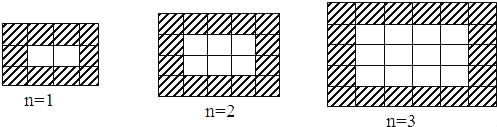
(1)在第n个图中,第一横行共 块瓷砖,第一竖列共有 块瓷砖;(均用含n的代数式表示)铺设地面所用瓷砖的总块数为 (用含n的代数式表示,n表示第n个图形)
(2)上述铺设方案,铺一块这样的长方形地面共用了506块瓷砖,求此时n的值;
(3)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF

(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是边长为1的正方形ABCD的对角线BD上一动点,点E从点B向点D运动(与点B,D不重合),过点E作直线GH∥BC,交AB于点G,交CD于点H,EF⊥AE,交CD(或CD的延长线)于点F.
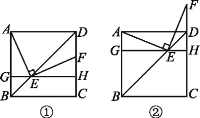
(1)如图①,求证:△AGE≌△EHF.
(2)在点E的运动过程中(如图①,②),四边形AFHG的面积是否会发生变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABD与△GDF都是等腰直角三角形,BD与DF均为斜边(BD<DF).
(1)如图1,B,D,F在同一直线上,过F作MF⊥GF于点F,取MF=AB,连结AM交BF于点H,连结GA,GM.
①求证:AH=HM;
②请判断△GAM的形状,并给予证明;
③请用等式表示线段AM,BD,DF的数量关系,并说明理由.
(2)如图2,GD⊥BD,连结BF,取BF的中点H,连结AH并延长交DF于点M,请用等式直接写出线段AM,BD,DF的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
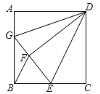
【题目】如图,已知正方形ABCD的边长为6,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 在以上4个结论中,正确的有( )
在以上4个结论中,正确的有( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将抛物线y=mx2﹣x﹣m(m≠0)在直线x=﹣1与直线x=1之间的部分记作图象C,对于图象C上任意一点P(a,b)均有﹣1≤b≤1成立,则m的取值范围是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点C的坐标为(
),点C的坐标为(![]() ,
,![]() ).
).
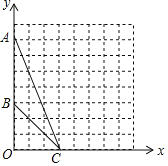
(1)在图中作出![]() 的外接圆(利用格图确定圆心);
的外接圆(利用格图确定圆心);
(2)圆心坐标为 _____;外接圆半径![]() 为 _____;
为 _____;
(3)若在![]() 轴的正半轴上有一点
轴的正半轴上有一点![]() ,且
,且![]() ,则点
,则点![]() 的坐标为 _____.
的坐标为 _____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com