
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点C的坐标为(
),点C的坐标为(![]() ,
,![]() ).
).
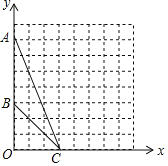
(1)在图中作出![]() 的外接圆(利用格图确定圆心);
的外接圆(利用格图确定圆心);
(2)圆心坐标为 _____;外接圆半径![]() 为 _____;
为 _____;
(3)若在![]() 轴的正半轴上有一点
轴的正半轴上有一点![]() ,且
,且![]() ,则点
,则点![]() 的坐标为 _____.
的坐标为 _____.
【答案】(1)确定圆心,画出圆见解析;(2)圆心坐标(5,5),半径为![]() ;(3)点D的坐标(7,0).
;(3)点D的坐标(7,0).
【解析】
(1)分别作三角形任意两边的垂直平分线,其交点即为圆心,到三角形三顶点的距离为半径作圆即可;(2)通过A,B,C三点坐标分别算出AB和BC的垂直平分线解析式,交点即为圆心,根据勾股定理算出圆心到C点的距离即为半径;(3)要使在![]() 轴的正半轴上有一点
轴的正半轴上有一点![]() ,且
,且![]() ,根据圆周角定理知圆与x轴的另一交点即为D,设D点坐标为(x,0),根据ED=r解出即可.
,根据圆周角定理知圆与x轴的另一交点即为D,设D点坐标为(x,0),根据ED=r解出即可.
(1)分别作三角形任意两边的垂直平分线,其交点即为圆心,到三角形三顶点的距离为半径作圆即可;
(2)∵点![]() 的坐标为(0,7),点
的坐标为(0,7),点![]() 的坐标为(0,3),点C的坐标为(3,0),
的坐标为(0,3),点C的坐标为(3,0),
∴AB的垂直平分线为y=5,
设BC的解析式为y=kx+b,把B(0,3),C(3,0)代入解得y=-x+3,则BC的垂直平分线的k=1,BC的中点坐标为(![]() ),则BC的垂直平分线为y=x,
),则BC的垂直平分线为y=x,
则y=5与y=x的交点为(5,5),故圆心为(5,5),
记圆心为点E,则EC=![]() =
=![]() ,即半径r=
,即半径r=![]() ;
;
(3)要使在x轴的正半轴上有一点D,且![]() ,根据圆周角定理知圆与x轴的另一交点即为D,设D点坐标为(x,0),则ED=
,根据圆周角定理知圆与x轴的另一交点即为D,设D点坐标为(x,0),则ED=![]() =
=![]() ,解得x1=3,x2=7,x=3为C点,则D点坐标为(7,0).
,解得x1=3,x2=7,x=3为C点,则D点坐标为(7,0).


科目:初中数学 来源: 题型:
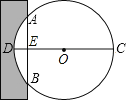
【题目】《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材在墙中,不知其大小用锯子去锯这个木材,锯口深DE=1寸,锯道长AB=10寸,问这块圆形木材的直径是多少?”
查看答案和解析>>
科目:初中数学 来源: 题型:
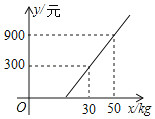
【题目】某旅客携带xkg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量xkg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量xkg的对应关系.
行李的重量xkg | 快递费 |
不超过1kg | 10元 |
超过1kg但不超过5kg的部分 | 3元/kg |
超过5kg但不超过15kg的部分 | 5元/kg |
(1)如果旅客选择单托运,求可携带的免费行李的最大重量为多少kg?
(2)如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量xkg之间的函数关系式;
(3)某旅客携带25kg的行李,设托运mkg行李(10≤m<24,m为正整数),剩下的行李选择快递,当m为何值时,总费用y的值最小?并求出其最小值是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
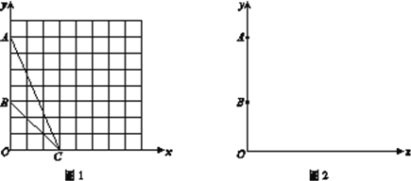
【题目】小明同学在学习与圆有关的角时了解到:在同圆或等圆中,同弧(或等弧)所对的圆周角相等.如图,点A、B、C、D均为⊙O上的点,则有∠C=∠D.
小明还发现,若点E在⊙O外,且与点D在直线AB同侧,则有∠D >∠E. 请你参考小明得出的结论,解答下列问题:
(1)如图1,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0) .①在图1中作出△ABC的外接圆(保留必要的作图痕迹,不写作法);
②若在![]() 轴的正半轴上有一点D,且∠ACB =∠ADB,则点D的坐标为________;
轴的正半轴上有一点D,且∠ACB =∠ADB,则点D的坐标为________;
(2) 如图2,在平面直角坐标系xOy中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0.点P为![]() 轴正半轴上的一个动点,当∠APB达到最大时,直接写出此时点P的坐标.
轴正半轴上的一个动点,当∠APB达到最大时,直接写出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
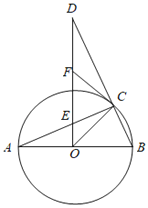
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:AC=DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边![]() 的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线
的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线![]() 是经过点P的一条直线,把
是经过点P的一条直线,把![]() 沿直线
沿直线![]() 折叠,点B的对应点是点
折叠,点B的对应点是点![]() .
.
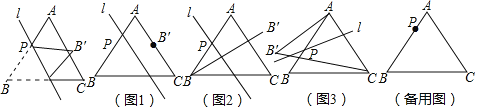
(1)如图1,当![]() 时,若点
时,若点![]() 恰好在AC边上,则
恰好在AC边上,则![]() 的长度为 ;
的长度为 ;
(2)如图2,当![]() 时,若直线
时,若直线![]() ,则
,则![]() 的长度为 ;
的长度为 ;
(3)如图3,点P在AB边上运动过程中,若直线![]() 始终垂直于AC,
始终垂直于AC,![]() 的面积是否变化?若变化,说明理由;若不变化,求出面积;
的面积是否变化?若变化,说明理由;若不变化,求出面积;
(4)当![]() 时,在直线
时,在直线![]() 变化过程中,求
变化过程中,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O是Rt△ABC的外接圆,点D是O上的一个动点,且C,D位于AB的两侧,联结AD,BD,过点C作CE⊥BD,垂足为E。延长CE交O于点F,CA,FD的延长线交于点P。
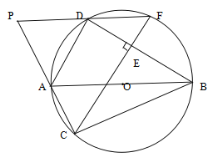
求证:(1)弧AF=弧DC;
(2)△PAD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣3x+m=0的两实数根是( )
A. x1=1,x2=﹣1B. x1=1,x2=3C. x1=1,x2=2D. x1=1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
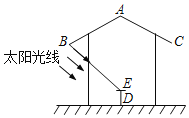
【题目】公园内一凉亭,凉亭顶部是一圆锥形的顶盖,立柱垂直于地面,在凉亭内中央位置有一圆形石桌,某数学研究性学习小组,将此凉亭作为研究对象,并绘制截面示意图,其中顶盖母线AB与AC的夹角为124°,凉亭顶盖边缘B、C到地面的距离为2.4米,石桌的高度DE为0.6米,经观测发现:当太阳光线与地面的夹角为42°时,恰好能够照到石桌的中央E处(A、E、D三点在一条直线上),请你求出圆锥形顶盖母线AB的长度.(结果精确到0.1m)(参考数据:sin62°≈0.88,tan42°≈0.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com