
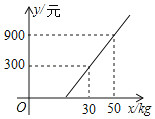
����Ŀ��ij�ÿ�Я��xkg������˷ɻ����ǻ�ǰ���ÿͿ�ѡ�����˻���������˷�y1(Ԫ)����������xkg�Ķ�Ӧ��ϵ����ͼ��ʾ��һ�κ���ͼ��ȷ�����±��г��˿�ݷ�y2(Ԫ)����������xkg�Ķ�Ӧ��ϵ��
���������xkg | ��ݷ� |
������1kg | 10Ԫ |
����1kg��������5kg�IJ��� | 3Ԫ/kg |
����5kg��������15kg�IJ��� | 5Ԫ/kg |
(1)����ÿ�ѡ�����ˣ����Я�������������������Ϊ����kg��
(2)����ÿ�ѡ���ݣ���1��x��15ʱ��ֱ��д����ݷ�y2(Ԫ)�����������xkg֮��ĺ�����ϵʽ��
(3)ij�ÿ�Я��25kg�����������mkg����(10��m��24��mΪ������)��ʣ�µ�����ѡ���ݣ���mΪ��ֵʱ���ܷ���y��ֵ��С�����������Сֵ�Ƕ���Ԫ��
���𰸡�(1)��Я�������������������Ϊ20kg��(2)y2��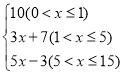 ��(3)������20kg�����5kg����ʱ���ܷ������٣����ٷ���Ϊ22Ԫ.
��(3)������20kg�����5kg����ʱ���ܷ������٣����ٷ���Ϊ22Ԫ.
��������
(1)�۲�ͼ���ҳ���������꣬���ô���ϵ������������˷�y1(Ԫ)����������xkg�ĺ�����ϵʽ����y1��0���뺯����ϵʽ�м��ɵó����ۣ�
(2)���ݱ����е����ݣ���x��1��1��x��5��5��x��15�������ҳ���ݷ�y2(Ԫ)����������xkg�ĺ�����ϵʽ��
(3)��10��m��20�Լ�20��m��24��������ҳ�y����m�ĺ�����ϵʽ������һ�κ��������ʿ��ҳ�y��ȡֵ��Χ���ҳ���yȡ��Сֵʱm��ֵ���ɵó����ۣ�
�⣺(1)�����˷�y1(Ԫ)����������xkg�ĺ�����ϵʽΪy1��kx+b��
��(30��300)��(50��900)����y1��kx+b��![]() ����ã�
����ã�![]() ��
��
�����˷�y1(Ԫ)����������xkg�ĺ�����ϵʽΪy1��30x��600��
��y1��30x��600��0ʱ��x��20��
�𣺿�Я�������������������Ϊ20kg��
(2)��������ã���0��x��1ʱ��y2��10��
��1��x��5ʱ��y2��10+3(x��1)��3x+7��
��5��x��15ʱ��y2��10+3��(5��1)+5(x��5)��5x��3��
������������ݷ�y2(Ԫ)����������xkg�ĺ�����ϵʽΪy2��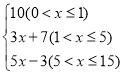 ��
��
(3)��10��m��20ʱ��5��25��m��15��
��y��y1+y2��0+5��(25��m)��3����5m+122��
��10��m��20��
��22��y��72��
��20��m��24ʱ��1��25��m��5��
��y��y1+y2��30m��600+3��(25��m)+7��27m��518��
��20��m��24��
��22��y��130��
���Ͽ�֪����m��20ʱ���ܷ���y��ֵ��С����СֵΪ22��
�𣺵�����20kg�����5kg����ʱ���ܷ������٣����ٷ���Ϊ22Ԫ��
�ʴ�Ϊ��(1)��Я�������������������Ϊ20kg��(2)y2��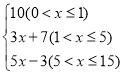 ��(3)������20kg�����5kg����ʱ���ܷ������٣����ٷ���Ϊ22Ԫ.
��(3)������20kg�����5kg����ʱ���ܷ������٣����ٷ���Ϊ22Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����������ABCD�У���E��F�ֱ���BC��CD�ϣ�AE = AF

��1����֤��BE = DF��
��2������AC��EF�ڵ�O���ӳ�OC����M��ʹOM = OA������EM��FM���ж��ı���AEMF��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
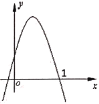
����Ŀ�����κ���![]() ��ͼ����ͼ��ʾ�������н��ۣ�
��ͼ����ͼ��ʾ�������н��ۣ�
�� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������ȷ�ĸ����ǣ� ��
������ȷ�ĸ����ǣ� ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y��mx2��x��m��m��0����ֱ��x����1��ֱ��x��1֮��IJ��ּ���ͼ��C������ͼ��C������һ��P��a��b�����Щ�1��b��1��������m��ȡֵ��Χ��___��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y��ax2+c��a��0����x�ύ�ڵ�A�͵�B��![]() ��0������y�ύ�ڵ�C��0��2������P��2��t���Ǹ���������һ�㣮
��0������y�ύ�ڵ�C��0��2������P��2��t���Ǹ���������һ�㣮

��1����������ߵĽ���ʽ��t��ֵ��
��2������D��y����һ�㣬�߶�PD�Ƶ�D��ʱ����ת90����P�Ķ�Ӧ��P��ǡ��Ҳ���ڴ��������ϣ����D�����ꣻ
��3����ͼ2��ֱ��l��y��kx+b������������M��N���㣬������MC��NC�����P��ֱ��l�ľ�����d����d�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
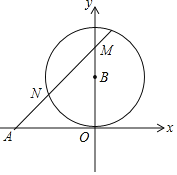
����Ŀ����ͼ����֪A����2��0������B��0��1��ΪԲ�ģ�OB��Ϊ�뾶����B��N����B��һ�����㣬ֱ��AN��y����M�㣬���AOM��������ֵ�ǣ�������
A. 2B. ![]() C. 4D.
C. 4D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
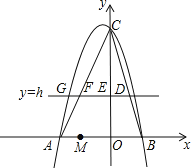
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+bx+6������A����3��0���͵�B��2��0����ֱ��y��h��hΪ��������0��h��6����BC���ڵ�D����y�ύ�ڵ�E����AC���ڵ�F��
��1���������ߵĽ���ʽ��
��2������AE����hΪ��ֵʱ����AEF��������
��3����֪һ����M����2��0�����ʣ��Ƿ����������ֱ��y��h��ʹ��BDM�ǵ��������Σ������ڣ������h��ֵ�͵�D�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���
�У���![]() ������Ϊ��
��������![]() ��
��![]() ������
������![]() ��������
��������![]() ��
��![]() ������C��������
������C��������![]() ��
��![]() ����
����
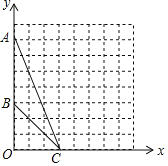
��1����ͼ������![]() �����Բ(���ø�ͼȷ��Բ��)��
�����Բ(���ø�ͼȷ��Բ��)��
��2��Բ������Ϊ _____�����Բ�뾶![]() Ϊ _____��
Ϊ _____��
��3������![]() �������������һ��
�������������һ��![]() ����
����![]() �����
�����![]() ������Ϊ _____��
������Ϊ _____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ÿһͼ�������ɸ���С��ͬ�����Σ���1��ͼ����1�����Σ���2��ͼ����3�����Σ���3��ͼ����5�����Σ������n��ͼ����2019�����Σ���n��_____��
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com