
【题目】如图1,抛物线y=ax2+c(a≠0)与x轴交于点A和点B(![]() ,0),与y轴交于点C(0,2),点P(2,t)是该抛物线上一点.
,0),与y轴交于点C(0,2),点P(2,t)是该抛物线上一点.

(1)求此抛物线的解析式及t的值;
(2)若点D是y轴上一点,线段PD绕点D逆时针旋转90°后,点P的对应点P′恰好也落在此抛物线上,求点D的坐标;
(3)如图2,直线l:y=kx+b交该抛物线于M、N两点,且满足MC⊥NC,设点P到直线l的距离是d,求d的最大值.
【答案】(1)y=﹣x2+2,t=﹣2;(2)点D的坐标为(0,﹣1)或(0,﹣4);(3)当∠RPK=0°时,d取得最大值为![]() .
.
【解析】
(1)已知抛物线上的点B、C坐标,用待定系数法即求得解析式;把P的横坐标代入解析式,即求得纵坐标t的值;
(2)按点P'在y轴左侧或右侧画出两种情况的图形,分别作点P、P'与y轴的垂线段PE、P'F,易证△DFP'≌△PED,由全等三角形对应边相等,可用含d的式子表示P'F与FD,进而用d表示点P'的坐标,即可求解;
(3)tan∠CNH=tan∠GCM,即:![]() ,即:
,即:![]() ,-x1x2=4-2y1-2y2+y1y2,整理得:b2-3b+2=0,解得:b=1,即可求解.
,-x1x2=4-2y1-2y2+y1y2,整理得:b2-3b+2=0,解得:b=1,即可求解.
解:(1)∵抛物线y=ax2+c过点B(![]() ,0)与点C(0,2),
,0)与点C(0,2),
∴ ![]() 解得:
解得:![]() ,
,
∴抛物线解析式为y=﹣x2+2,
∵点P(2,t)是该抛物线上一点,
∴t=﹣4+2=﹣2;
(2)过点P作PE⊥y轴于点E,过点P'作P'F⊥y轴于点F,
∴∠PED=∠DFP'=90°,
∵P(2,﹣2),
∴PE=2,OE=2,
设D(0,d),
①若d>﹣2,即点D在点P上方,则点P'在y轴右侧,如图1,

∴DE=d﹣(﹣2)=d+2,
∵PD绕点D逆时针旋转90°得到P'D,
∴∠PDP'=90°,PD=P'D,
∴∠FDP'+∠PDE=∠FDP'+∠DP'F=90°,
∴∠PDE=∠DP'F,
在△DFP'与△PED中,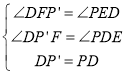 ,
,
∴△DFP'≌△PED(AAS),
∴DF=PE=2,FP'=DE=d+2,
∴P'(d+2,d+2),
∵点P'也在抛物线上,
∴﹣(d+2)2+2=d+2,
解得:d1=﹣4(舍去),d2=﹣1,
∴D(0,﹣1),
②若d<﹣2,即点D在点P下方,则点P'在y轴左侧,如图2,

∴DE=﹣2﹣d,
同理可证:△DFP'≌△PED,
∴DF=PE=2,FP'=DE=﹣2﹣d,
∴P'(d+2,d+2),
∴﹣(﹣
解得:d1=﹣4,d2=﹣1(舍去),
∴D(0,﹣4),
综上所述,点D的坐标为(0,﹣1)或(0,﹣4);
(3)设点M、N的坐标分别为:(x1,y1)、(x2、y2),直线l与y轴交于点R,
联立y=﹣x2+2,y=kx+b并整理得:
x2+kx+(b﹣2)=0,
x1+x2=﹣k,x1x2=b﹣2,
y1=kx1+b,y2=kx2+b,
故点C作x轴的平行线GH,分别过点M、N作y轴的平行线交GH于点G、H,
∵MC⊥NC,∴∠GCM+∠HCN=90°,∠HCN+∠CNH=90°,
∴∠CNH=∠GCM,
∴tan∠CNH=tan∠GCM,即:![]() ,
,
即:![]() ,
,
﹣x1x2=4﹣2y1﹣2y2+y1y2,其中x1+x2=﹣k,x1x2=b﹣2,y1=kx1+b,y2=kx2+b,
整理得:b2﹣3b+2=0,整理得:b=1或2(舍去2),
故:b=1,
则点R(0,1),而点P(2,﹣2),
过点P作PK⊥l交于点K,
则d=PK=RPcos∠RPK,
当∠RPK=0°时,d取得最大值为:PR=![]() .
.


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
【题目】(1)操作发现:
如图①,在Rt△ABC中,∠C=2∠B=90°,点D是BC上一点,沿AD折叠△ADC,使得点C恰好落在AB上的点E处.请写出AB、AC、CD之间的关系 ;
(2)问题解决:
如图②,若(1)中∠C≠90°,其他条件不变,请猜想AB、AC、CD之间的关系,并证明你的结论;
(3)类比探究:
如图③,在四边形ABCD中,∠B=120°,∠D=90°,AB=BC,AD=DC,连接AC,点E是CD上一点,沿AE折叠,使得点D正好落在AC上的F处,若BC=![]() ,直接写出DE的长.
,直接写出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年春季,莒县某服装商店分两次从批发市场购进同一款服装,数量之比是2:3,且第一、二次进货价分别为每件50元、40元,总共付了6600元的货款.
(1)求第一、二次购进服装的数量分别是多少件?
(2)由于该款服装刚推出时,很受欢迎,按每件60元销售了x件;后来,由于该服装滞销,为了及时处理库存,缓解资金压力,其剩余部分的按每件30元全部售完.当x的值至少为多少时,该服装商店才不会亏本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.
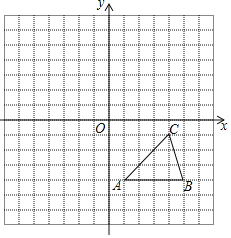
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O对称的△A2B2C2;
(3)△A1B1C1与△A2B2C2关于某个点对称,则这个点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
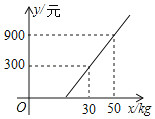
【题目】某旅客携带xkg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量xkg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量xkg的对应关系.
行李的重量xkg | 快递费 |
不超过1kg | 10元 |
超过1kg但不超过5kg的部分 | 3元/kg |
超过5kg但不超过15kg的部分 | 5元/kg |
(1)如果旅客选择单托运,求可携带的免费行李的最大重量为多少kg?
(2)如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量xkg之间的函数关系式;
(3)某旅客携带25kg的行李,设托运mkg行李(10≤m<24,m为正整数),剩下的行李选择快递,当m为何值时,总费用y的值最小?并求出其最小值是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
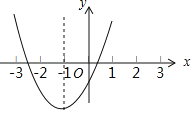
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a﹣b+c<0;⑤3a+c>0.其中正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
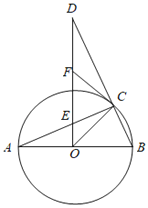
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:AC=DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周未,小丽骑自行车从家出发到野外郊游,从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地,小丽离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地,如图是她们距乙地的路程y(km)与小丽离家时间x(h)的函数图象.
(1)小丽骑车的速度为 km/h,H点坐标为 ;
(2)求小丽游玩一段时间后前往乙地的过程中y与x的函数关系;
(3)小丽从家出发多少小时后被妈妈追上?此时距家的路程多远.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com