
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.
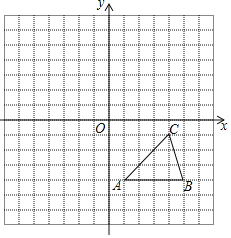
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O对称的△A2B2C2;
(3)△A1B1C1与△A2B2C2关于某个点对称,则这个点的坐标为 .
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,![]() 、
、![]() 、
、![]() 分别是菱形ABCD的两条对角线长和边长,这时我们把关于
分别是菱形ABCD的两条对角线长和边长,这时我们把关于![]() 的形如“
的形如“![]() ”的一元二次方程称为“菱系一元二次方程”.请解决下列问题:
”的一元二次方程称为“菱系一元二次方程”.请解决下列问题:

(1)填空:①当![]() ,
,![]() 时,
时,![]() .
.
②用含![]() ,
,![]() 的代数式表示
的代数式表示![]() 值,
值,![]() .
.
(2)求证:关于![]() 的“菱系一元二次方程”
的“菱系一元二次方程”![]() 必有实数根;
必有实数根;
(3)若![]() 是“菱系一元二次方程”
是“菱系一元二次方程”![]() 的一个根,且菱形的面积是25,BE是菱形ABCD的AD边上的高,求BE的值.
的一个根,且菱形的面积是25,BE是菱形ABCD的AD边上的高,求BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段BE为何值时,线段AM最短,最短是多少?
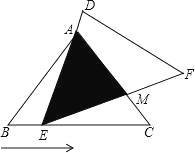
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+c(a≠0)与x轴交于点A和点B(![]() ,0),与y轴交于点C(0,2),点P(2,t)是该抛物线上一点.
,0),与y轴交于点C(0,2),点P(2,t)是该抛物线上一点.

(1)求此抛物线的解析式及t的值;
(2)若点D是y轴上一点,线段PD绕点D逆时针旋转90°后,点P的对应点P′恰好也落在此抛物线上,求点D的坐标;
(3)如图2,直线l:y=kx+b交该抛物线于M、N两点,且满足MC⊥NC,设点P到直线l的距离是d,求d的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校喜迎中华人民共和国成立70周年,将举行以“歌唱祖国”为主题的歌咏比赛,需要在文具店购买国旗图案贴纸和小红旗发给学生做演出道具.已知毎袋贴纸有50张,毎袋小红旗有20面,贴纸和小红旗需整袋购买,每袋贴纸价格比每袋小红旗价格少5元,用150元购买贴纸所得袋数与用200元购买小红旗所得袋数相同.
(1)求每袋国旗图案贴纸和每袋小红旗的价格各是多少元?
(2)如果给每位演出学生分发国旗图案贴纸2张,小红旗1面.设购买国旗图案贴纸![]() 袋(
袋(![]() 为正整数),则购买小红旗多少袋能恰好配套?请用含
为正整数),则购买小红旗多少袋能恰好配套?请用含![]() 的代数式表示.
的代数式表示.
(3)在文具店累计购物超过800元后,超出800元的部分可享受8折优惠.学校按(2)中的配套方案购买,共支付![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?
的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
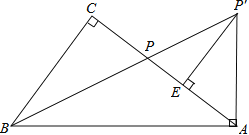
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当![]() ,BP′=
,BP′=![]() 时,求线段AB的长.
时,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛德物线y=![]() +1有下性质:该抛物线上任意一点到定点F(0,2)的距离与到轴的距离始终相等,如图,点M的坐标为(
+1有下性质:该抛物线上任意一点到定点F(0,2)的距离与到轴的距离始终相等,如图,点M的坐标为(![]() ,3),P是抛物线y=
,3),P是抛物线y=![]() +1上一个动点,则△PMF周长的最小值是_____.
+1上一个动点,则△PMF周长的最小值是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com