
����Ŀ����ͼ��������ABCD�У�![]() ��
��![]() ��
��![]() �ֱ�������ABCD�������Խ��߳��ͱ߳�����ʱ���ǰѹ���
�ֱ�������ABCD�������Խ��߳��ͱ߳�����ʱ���ǰѹ���![]() ��������
��������![]() ����һԪ���η��̳�Ϊ����ϵһԪ���η������������������⣺
����һԪ���η��̳�Ϊ����ϵһԪ���η������������������⣺

��1����գ�����![]() ��
��![]() ʱ��
ʱ��![]() ��
��
���ú�![]() ��
��![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ֵ��
ֵ��![]() ��
��
��2����֤������![]() ������ϵһԪ���η�����
������ϵһԪ���η�����![]() ����ʵ������
����ʵ������
��3����![]() ������ϵһԪ���η�����
������ϵһԪ���η�����![]() ��һ�����������ε������25��BE������ABCD��AD���ϵĸߣ���BE��ֵ��
��һ�����������ε������25��BE������ABCD��AD���ϵĸߣ���BE��ֵ��
���𰸡���1����5����![]() ����2������������3��
����2������������3��![]()
��������
��1�����ͼ�Σ��������εĶԽ�����ƽ���Լ����ɶ������ɵõ����ۣ�
��2�����������ϣ�1���ТڵĽ��ۼ��ɽ�����⣻
��3�����ݷ��̸��Ķ���ó�m��n��t�Ĺ�ϵ����ϣ�1���ТڵĽ��۽��л����ٸ������������25�����ɵó�t��ֵ�������ó����ۣ�
��1���ٵ�m=6��n=8ʱ��AO=4��OB=3����t=AB=![]() =5��
=5��
�ڡ�AO=![]() ��OB=
��OB=![]() ����t2=AB2=
����t2=AB2=![]() ��
��
�ʴ�Ϊ��5��![]() ��
��
��2��![]()
���a=m��b=![]() t��c=n����
t��c=n����![]() ��
��
��![]() ����
����![]()
![]() �������
�������![]() ������ϵһԪ���η�����
������ϵһԪ���η�����![]() ����ʵ������
����ʵ������
��3����![]() ������ϵһԪ���η�����
������ϵһԪ���η�����![]() ��һ��������
��һ��������![]() ����
����![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��
�����������25����![]() ����
����![]() ����ã�
����ã�![]() ����
����![]() ����
����![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ͼ1��ͼ2�����ı���ABCD�DZ߳�Ϊ4�������Σ���E���߶�BC�ϣ���AEF=90��,��EF�����������ƽ����CP�ڵ�F����BC���ӳ����ڵ�N, FN��BC.
��1������E��BC���е㣨��ͼ1����AE��EF�����
��2����E��BC���˶�ʱ����ͼ2������BE=x����ECF�����Ϊy��
����y��x�ĺ�����ϵʽ��
�ڵ�xȡ��ֵʱ��y�����ֵ�������������ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�λ����Ϊ1�������������н���һֱ������ϵ��һ��Բ�����������A��B��C����������ͼ�н������в��������½���������ţ�.
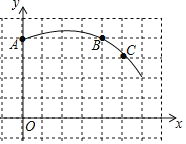
��1����������������Բ������Բ��Բ��D���λ�ã���д��D�������Ϊ�� ��
��2������AD��CD�����D�İ뾶Ϊ�� ����ADC�Ķ���Ϊ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������ABCD�Ķ���A������Ϊ(��1��1)����B��x���������ϣ���D�ڵ�������˫����y��![]() �ϣ�����C��CE��x�ύ˫�����ڵ�E����CE�ij�Ϊ( )
�ϣ�����C��CE��x�ύ˫�����ڵ�E����CE�ij�Ϊ( )

A. ![]() B.
B. ![]() C. 3.5D. 5
C. 3.5D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
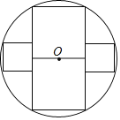
����Ŀ����ͼ��Բ��ֽƬ��O�뾶Ϊ![]() ���������ڼ���2���߳���ȵ���������Σ�����ʣ�ಿ�ּ���2���߳���ȵ���������Σ���ڶ��μ����������εı߳���______��
���������ڼ���2���߳���ȵ���������Σ�����ʣ�ಿ�ּ���2���߳���ȵ���������Σ���ڶ��μ����������εı߳���______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019�괺��������ij��װ�̵�����δ������г�����ͬһ���װ������֮����2��3���ҵ�һ�����ν����۷ֱ�Ϊÿ��50Ԫ��40Ԫ���ܹ�����6600Ԫ�Ļ��
��1�����һ�����ι�����װ�������ֱ��Ƕ��ټ���
��2�����ڸÿ��װ���Ƴ�ʱ�����ܻ�ӭ����ÿ��60Ԫ������x�������������ڸ÷�װ������Ϊ�˼�ʱ������棬�����ʽ�ѹ������ʣ�ಿ�ֵİ�ÿ��30Ԫȫ�����꣮��x��ֵ����Ϊ����ʱ���÷�װ�̵�Ų��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
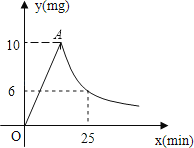
����Ŀ���Ϸ���ʮ����ΪԤ���^�����������Խ��ҽ��С�ҩ����������֪ҩ����ȼ���ͷŹ����У����ڿ�����ÿ������ҩ��![]() �����ˣ���ȼ��ʱ��
�����ˣ���ȼ��ʱ��![]() �����ӣ�֮��Ĺ�ϵ��ͼ��ʾ����ͼ���߶�
�����ӣ�֮��Ĺ�ϵ��ͼ��ʾ����ͼ���߶�![]() ��˫������
��˫������![]() �㼰���Ҳ�IJ��֣�������ͼ����ʾ��Ϣ������������⣺
�㼰���Ҳ�IJ��֣�������ͼ����ʾ��Ϣ������������⣺
��1��д����ҩ���ͷſ�ʼ��![]() ��
��![]() ֮��ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
֮��ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
��2���ݲⶨ��ֻ�е�������ÿ�����ĺ�ҩ��������![]() ����ʱ����Ԥ���������ã������ٳ�������
����ʱ����Ԥ���������ã������ٳ�������![]() �������ϣ�������ȫɱ�����ֲ�����������������Ƿף�
�������ϣ�������ȫɱ�����ֲ�����������������Ƿף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ�
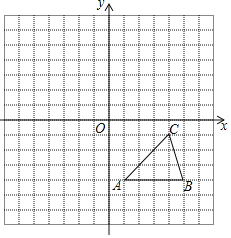
��1������ABC����ƽ��5����λ��õ���Ӧ����A1B1C1��������A1B1C1��
��2����������ABC����ԭ��O�ԳƵ���A2B2C2��
��3����A1B1C1����A2B2C2����ij����Գƣ�������������Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,![]() ��
��![]() �ı�
�ı�![]() ���е�,��
���е�,��![]() �ӳ����ϵĵ�
�ӳ����ϵĵ�![]() ��
��![]() �Ĵ���
�Ĵ���![]() ,
,![]() ����,
����,![]() ��
��![]() ���ӳ����ཻ�ڵ�
���ӳ����ཻ�ڵ�![]() ,��
,��![]() ��
��![]() ��,
��,![]() ,
,![]() ��
��![]() ��
��
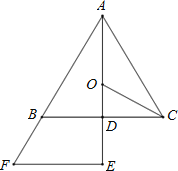
��1��֤����![]() ��
��
��2��֤������![]() ��
��![]() �����Բ��Բ�ģ�
�����Բ��Բ�ģ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com