
【题目】如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
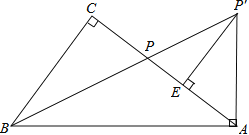
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当![]() ,BP′=
,BP′=![]() 时,求线段AB的长.
时,求线段AB的长.
【答案】解:(1)证明:∵AP′是AP旋转得到,∴AP=AP′。∴∠APP′=∠AP′P。
∵∠C=90°,AP′⊥AB,∴∠CBP+∠BPC=90°,∠ABP+∠AP′P=90°。
又∵∠BPC=∠APP′(对顶角相等)。∴∠CBP=∠ABP。
(2)证明:如图,过点P作PD⊥AB于D,
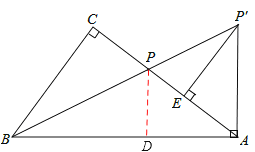
∵∠CBP=∠ABP,∠C=90°,∴CP=DP。
∵P′E⊥AC,∴∠EAP′+∠AP′E=90°。
又∵∠PAD+∠EAP′=90°,
∴∠PAD=∠AP′E。
在△APD和△P′AE中,
∵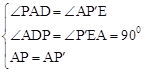 ,
,
∴△APD≌△P′AE(AAS)。∴AE=DP。∴AE=CP。
(3)∵![]() ,∴设CP=3k,PE=2k,则AE=CP=3k,AP′=AP=3k+2k=5k。
,∴设CP=3k,PE=2k,则AE=CP=3k,AP′=AP=3k+2k=5k。
在Rt△AEP′中,![]() ,
,
∵∠C=90°,P′E⊥AC,∴∠CBP+∠BPC=90°,∠EP′P+∠P′PE=90°。
∵∠BPC=∠EPP′(对顶角相等),∴∠CBP=∠P′PE。
又∵∠BAP′=∠P′EP=90°,∴△ABP′∽△EPP′。
∴![]() 。即
。即![]() 。∴
。∴![]() 。
。
在Rt△ABP′中,![]() ,即
,即![]() 。
。
解得AB=10
【解析】
试题:(1)根据旋转的性质可得AP=AP′,根据等边对等角的性质可得∠APP′=∠AP′P,再根据等角的余角相等证明即可;
(2)过点P作PD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CP=DP,然后求出∠PAD=∠AP′E,利用“角角边”证明△APD和△P′AE全等,根据全等三角形对应边相等可得AE=DP,从而得证;
(3)设CP=3k,PE=2k,表示出AE=CP=3k,AP′=AP=5k,然后利用勾股定理列式求出P′E=4k,再求出△ABP′和△EPP′相似,根据相似三角形对应边成比例列式求出P′A=![]() AB,然后在Rt△ABP′中,利用勾股定理列式求解即可.
AB,然后在Rt△ABP′中,利用勾股定理列式求解即可.
试题解析:(1)证明:∵AP′是AP旋转得到,
∴AP=AP′,
∴∠APP′=∠AP′P,
∵∠C=90°,AP′⊥AB,
∴∠CBP+∠BPC=90°,∠ABP+∠AP′P=90°,
又∵∠BPC=∠APP′,
∴∠CBP=∠ABP;
(2)证明:如图,过点P作PD⊥AB于D,
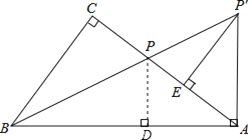
∵∠CBP=∠ABP,∠C=90°,
∴CP=DP,
∵P′E⊥AC,
∴∠EAP′+∠AP′E=90°,
又∵∠PAD+∠EAP′=90°,
∴∠PAD=∠AP′E,
在△APD和△P′AE中,
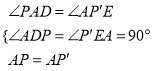 ,
,
∴△APD≌△P′AE(AAS),
∴AE=DP,
∴AE=CP;
(3)解:∵![]() ,
,
∴设CP=3k,PE=2k,
则AE=CP=3k,AP′=AP=3k+2k=5k,
在Rt△AEP′中,P′E=![]() =4k,
=4k,
∵∠C=90°,P′E⊥AC,
∴∠CBP+∠BPC=90°,∠EP′P+∠EPP′=90°,
∵∠BPC=∠EPP′,
∴∠CBP=∠EP′P,
又∵∠CBP=∠ABP,∴∠ABP=∠EP′P,
又∵∠BAP′=∠P′EP=90°,
∴△ABP′∽△EPP′,
∴![]() ,
,
即![]() ,
,
解得P′A=![]() AB,
AB,
在Rt△ABP′中,AB2+P′A2=BP′2,
即AB2+![]() AB2=(5
AB2=(5![]() )2,
)2,
解得AB=10.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=![]() 上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )
上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )

A. ![]() B.
B. ![]() C. 3.5D. 5
C. 3.5D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.
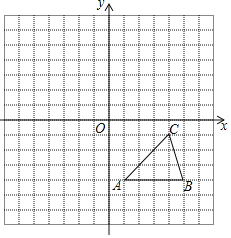
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O对称的△A2B2C2;
(3)△A1B1C1与△A2B2C2关于某个点对称,则这个点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
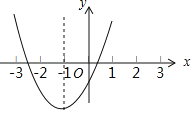
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a﹣b+c<0;⑤3a+c>0.其中正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
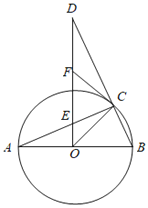
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:AC=DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步深化基教育课程改革,构建符合素质教育要求的学校课程体系,某学校自主开发了A书法、B阅读,C足球,D器乐四门校本选修课程供学生选择,每门课程被选到的机会均等.
(1)学生小红计划选修两门课程,请写出所有可能的选法;
(2)若学生小明和小刚各计划送修一门课程,则他们两人恰好选修同一门课程的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与![]() 轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com