
����Ŀ��С���о����κ���y=-(x-m)2-m+1(mΪ����)����ʱ���½��ۣ����������ͼ��Ķ���ʼ����ֱ��y=-x+1�ϣ��ڴ���һ��m��ֵ��ʹ�ú���ͼ��Ķ�����![]() ����������㹹�ɵ���ֱ�������Σ��۵�A(x1,y1)���B(x2,y2)�ں���ͼ���ϣ���x1<x2��x1+x2>2m����y1<y2���ܵ�-1<x<2ʱ��y��x�������������m��ȡֵ��ΧΪm��2���д�����۵�����ǣ� ��
����������㹹�ɵ���ֱ�������Σ��۵�A(x1,y1)���B(x2,y2)�ں���ͼ���ϣ���x1<x2��x1+x2>2m����y1<y2���ܵ�-1<x<2ʱ��y��x�������������m��ȡֵ��ΧΪm��2���д�����۵�����ǣ� ��
A. ��B. ��C. ��D. ��
���𰸡�C
��������
�Ѷ����������y=-x+1�����жϢ٣����ݹ��ɶ��������жϢڣ������ڶԳ�����ұ�y��x���������С���жϢۣ��������ڶԳ�����ұ�y��x�������������жϢ�.
�ѣ�m��-m+1������y=-x+1��-m+1=-m+1����=�ң��ʢ���ȷ��
��-(x-m)2-m+1=0ʱ��x1=![]() , x2=
, x2=![]() ,
,
��������![]() ����������㹹�ɵ���ֱ�������Σ�
����������㹹�ɵ���ֱ�������Σ�
��1-m+(1-m)2+1-m+(1-m)2=4(1-m)����m2-m=0��
��m=0��1ʱ�������һ��m��ֵ��ʹ�ú���ͼ��Ķ�����![]() ����������㹹�ɵ���ֱ�������Σ��ʢ���ȷ��
����������㹹�ɵ���ֱ�������Σ��ʢ���ȷ��
��x1<x2����x1��x2�ڶԳ����Ҳ�ʱ��
��-1<0, ���ڶԳ����Ҳ�y��x���������С����y1>y2���ʢ۴���
��-1<0, ���ڶԳ������y��x�����������
��m��2���ʢ���ȷ.
��ѡC.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC�Ķ���ֱ���A����3��2��B��0��4��C��0��2����
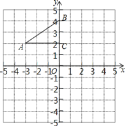
��1������ABC�Ե�CΪ��ת������ת180����������ת���Ӧ����A1B1C1��
��2���ֱ�����AB1��BA1�����ı���AB1A1B�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����A��B���������߲˻��أ������߲�700��.����A���ص��߲�ȫ�������������������B���ص��߲�ȫ�������������������ͬ.��A��B�����������ס������е��˷ѵ������±�:
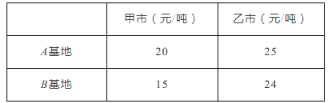
��1����A��B�����߲˻��ظ����߲˶��ٶ֣�
��2���ּ�����Ҫ�߲�260�֣�������Ҫ�߲�440��.���A��������![]() ���߲˵����У������������˿�ʹ���˷����٣�
���߲˵����У������������˿�ʹ���˷����٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��x��Ĵ��ߣ��ֱ�ֱ��
��x��Ĵ��ߣ��ֱ�ֱ��![]() ��C��D����
��C��D����![]() ������
������![]() ����O��C��D���㣮
����O��C��D���㣮
![]() �������ߵı���ʽ��
�������ߵı���ʽ��
![]() ��MΪֱ��OD�ϵ�һ�����㣬��M��x��Ĵ��߽��������ڵ�N�����Ƿ���������ĵ�M��ʹ����A��C��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ����ʱ��M�ĺ����ꣻ�������ڣ���˵�����ɣ�
��MΪֱ��OD�ϵ�һ�����㣬��M��x��Ĵ��߽��������ڵ�N�����Ƿ���������ĵ�M��ʹ����A��C��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ����ʱ��M�ĺ����ꣻ�������ڣ���˵�����ɣ�
![]() ��
��![]() ��CD����ƽ��
��CD����ƽ��![]() ��C���߶�CD�ϣ��Ҳ����D�غ�
��C���߶�CD�ϣ��Ҳ����D�غ�![]() ����ƽ�ƵĹ�����
����ƽ�ƵĹ�����![]() ��
��![]() �ص����ֵ������ΪS������S�����ֵ��
�ص����ֵ������ΪS������S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
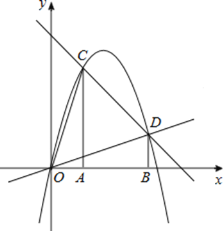
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��������y��3x2��2x��2���˶�������A��AC��x���ڵ�C����ACΪ�Խ���������ABCD������BD����Խ���BD����СֵΪ_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ijһ�������������¶��壺������ڳ���![]() ����������ĺ���ֵ
����������ĺ���ֵ![]() ��������
��������![]() ��
��![]() ����ô��������������Ͻ纯��������������������
����ô��������������Ͻ纯��������������������![]() �У�����Сֵ��Ϊ�����������ȷ�磮���磬����
�У�����Сֵ��Ϊ�����������ȷ�磮���磬����![]() ��
�� ![]() ��2����������Ͻ纯��������ȷ����2���������
��2����������Ͻ纯��������ȷ����2���������![]() ��
��![]() ��x��
��x��![]() ��
�� ![]() ��
��![]() ������ȷ����
������ȷ����![]() ���������������Сֵ������2
���������������Сֵ������2![]() ����
����![]() ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A. ![]() ��
��![]() B.
B. ![]() C.
C. ![]() ��
��![]() D.
D. ![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����в�Ҷר��������ijƷ�Ʋ�Ҷ�������Ϊÿǧ�� 240 Ԫ����ÿǧ�� 400 Ԫ���ۣ�ƽ��ÿ�ܿ��۳� 200 ǧ�ˣ����������г����鷢�֣�����ÿ���� 10 Ԫ����ƽ��ÿ�ܵ������������� 40 ǧ�ˣ�����ר������������Ʒ�Ʋ�ҶҪ��ƽ��ÿ�ܻ��� 41600 Ԫ����ش�
��1��ÿǧ�˲�ҶӦ���۶���Ԫ��
��2����ƽ��ÿ�ܻ������������£�Ϊ�����������ڹ˿ͣ�Ӯ���г����õ�Ӧ��ԭ�ۼ۵� ���۳��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���֪��C=90������B=55������D�ڱ�BC�ϣ�BD=2CD.���߶�BD ���ŵ�D��ʱ����ת��(0������180)�Ⱥ������Bǡ������Rt��ABC�ı��ϣ���ô��=__________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD �У�AB=4��AD=a����P��AD�ϣ���AP=2����E�DZ�AB�ϵĶ��㣬��PEΪ����ֱ�ǡ�EPF������PF��BC�ڵ�F������EF���������н��ۣ���tan��PFE=![]() ����a����СֵΪ10.������˵����ȷ����( )
����a����СֵΪ10.������˵����ȷ����( )
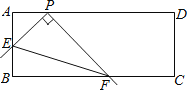
A.�٢ڶ���B.�٢ڶ���C.�ٶԢڴ�D.�ٴ��ڶ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com