
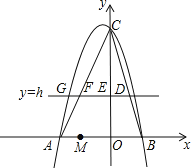
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+bx+6������A����3��0���͵�B��2��0����ֱ��y��h��hΪ��������0��h��6����BC���ڵ�D����y�ύ�ڵ�E����AC���ڵ�F��
��1���������ߵĽ���ʽ��
��2������AE����hΪ��ֵʱ����AEF��������
��3����֪һ����M����2��0�����ʣ��Ƿ����������ֱ��y��h��ʹ��BDM�ǵ��������Σ������ڣ������h��ֵ�͵�D�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2��x+6����2����h��3ʱ����AEF���������������� ![]() ����3�����ڣ���h��
����3�����ڣ���h��![]() ʱ����D������Ϊ��
ʱ����D������Ϊ��![]() ��
��![]() ������h��
������h��![]() ʱ����D������Ϊ��
ʱ����D������Ϊ��![]() ��
��![]() ����
����
��������
��1�����ô���ϵ�������ɽ�����⣮
��2��������ɵõ�E������Ϊ��0��h������F������Ϊ�� ![]() ��h��������S��AEF��
��h��������S��AEF��![]() OEFE��
OEFE��![]() h
h![]() ����
����![]() ��h��3��2+
��h��3��2+![]() �����ö��κ��������ʼ��ɽ�����⣮
�����ö��κ��������ʼ��ɽ�����⣮
��3�����ڣ��������������Σ��ֱ��г����̼��ɽ�����⣮
�⣺��ͼ��
��1����������y��ax2+bx+6������A����3��0���͵�B��2��0����
��![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪy����x2��x+6��
��2���߰�x��0����y����x2��x+6����y��6��
���C��������0��6����
�辭����A�͵�C��ֱ�ߵĽ���ʽΪy��mx+n����![]() ��
��
��� ![]() ��
��
�ྭ����A�͵�C��ֱ�ߵĽ���ʽΪ��y��2x+6��
�ߵ�E��ֱ��y��h�ϣ�
���E��������0��h����
��OE��h��
�ߵ�F��ֱ��y��h/span>�ϣ�
���F��������Ϊh��
��y��h����y��2x+6����h��2x+6��
���x��![]() ��
��
���F�������� ![]() ��h����
��h����
��EF��![]() ��
��
��S��AEF��![]() OEFE��
OEFE��![]() h
h![]() ����
����![]() ��h��3��2+
��h��3��2+![]() ��
��
�ߩ�![]() ��0��0��h��6��
��0��0��h��6��
�൱h��3ʱ����AEF����������������![]() ��
��
��3�����ڷ��������ֱ��y��h��
��B��2��0����C��0��6����
��ֱ��BC�Ľ���ʽΪy����3x+6����D��m����3m+6����
����BM��BDʱ����m��2��2+����3m+6��2��42��
���m��![]() ��
��![]() ����������
����������
��D��![]() ��
��![]() ������ʱh��
������ʱh��![]() ��
��
����MD��BMʱ����m+2��2+����3m+6��2��42��
���m��![]() ��2����������
��2����������
��D��![]() ��
��![]() ������ʱh��
������ʱh��![]() ��
��
����������������������ֱ��y��![]() ��y��
��y��![]() ��ʹ��BDM�ǵ��������Σ���h��
��ʹ��BDM�ǵ��������Σ���h��![]() ʱ����D������Ϊ��
ʱ����D������Ϊ��![]() ��
��![]() ������h��
������h��![]() ʱ����D������Ϊ��
ʱ����D������Ϊ��![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O����������A,B����������C,D,AC��BD���ڵ�E.
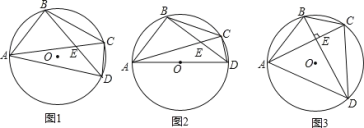
(1)��ͼ1����֤��EAEC=EBED��
(2)��ͼ2,��AB=BC��AD��O��ֱ������֤��ADAC=2BDBC��
(3) ��ͼ3����AC��BD����O��AD�ľ���Ϊ2����BC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����A=60��,AC=1��AB=2��BC�ij�;
��2����ͼ2������ABC�У���֤��:BC2=AC2+AB2-2AC![]() ABcosA.
ABcosA.
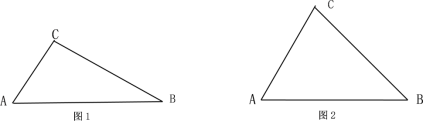
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
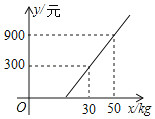
����Ŀ��ij�ÿ�Я��xkg������˷ɻ����ǻ�ǰ���ÿͿ�ѡ�����˻���������˷�y1(Ԫ)����������xkg�Ķ�Ӧ��ϵ����ͼ��ʾ��һ�κ���ͼ��ȷ�����±��г��˿�ݷ�y2(Ԫ)����������xkg�Ķ�Ӧ��ϵ��
���������xkg | ��ݷ� |
������1kg | 10Ԫ |
����1kg��������5kg�IJ��� | 3Ԫ/kg |
����5kg��������15kg�IJ��� | 5Ԫ/kg |
(1)����ÿ�ѡ�����ˣ����Я�������������������Ϊ����kg��
(2)����ÿ�ѡ���ݣ���1��x��15ʱ��ֱ��д����ݷ�y2(Ԫ)�����������xkg֮��ĺ�����ϵʽ��
(3)ij�ÿ�Я��25kg�����������mkg����(10��m��24��mΪ������)��ʣ�µ�����ѡ���ݣ���mΪ��ֵʱ���ܷ���y��ֵ��С�����������Сֵ�Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
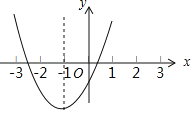
����Ŀ����֪���κ���y��ax2+bx+c��ͼ����ͼ����Գ���x����1���������н������b2��4ac����abc��0����2a+b��0����a��b+c��0����3a+c��0��������ȷ���۵������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��ѧϰ��Բ�йصĽ�ʱ�˽����ͬԲ���Բ�У�ͬ������Ȼ������Ե�Բ�ܽ��������ͼ����A��B��C��D��Ϊ��O�ϵĵ㣬���С�C=��D��
С�������֣�����E�ڡ�O�⣬�����D��ֱ��ABͬ�࣬���С�D >��E�� ����ο�С���ó��Ľ��ۣ�����������⣺
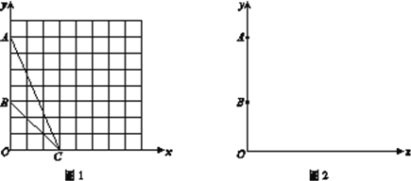
��1����ͼ1����ƽ��ֱ������ϵxOy�У���A������Ϊ(0,7)����B������Ϊ(0,3)����C������Ϊ(3,0) ������ͼ1��������ABC�����Բ��������Ҫ����ͼ�ۼ�����д��������
������![]() �������������һ��D���ҡ�ACB =��ADB�����D������Ϊ________��
�������������һ��D���ҡ�ACB =��ADB�����D������Ϊ________��
(2) ��ͼ2����ƽ��ֱ������ϵxOy�У���A������Ϊ(0,m)����B������Ϊ(0,n)������m>n>0����PΪ![]() ���������ϵ�һ�����㣬����APB�ﵽ���ʱ��ֱ��д����ʱ��P��������
���������ϵ�һ�����㣬����APB�ﵽ���ʱ��ֱ��д����ʱ��P��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬����O��OD��AB����BC���ӳ�����D����AC�ڵ�E��F��DE���е㣬����CF��
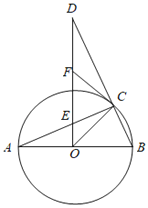
��1����֤��CF�ǡ�O�����ߣ�
��2������A��22.5������֤��AC��DC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪O��Rt��ABC�����Բ����D��O�ϵ�һ�����㣬��C��Dλ��AB�����࣬����AD��BD������C��CE��BD������ΪE���ӳ�CE��O�ڵ�F��CA��FD���ӳ��߽��ڵ�P��
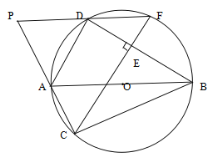
��֤����1����AF=��DC;
��2����PAD�ǵ���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�о�ѧ���Ŀ��మ���������ȡ��������ķ��������Ķ����˶������֡��������ĸ��������������ѧ������Ȥ���ã���������Ľ�����Ƴ�����������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
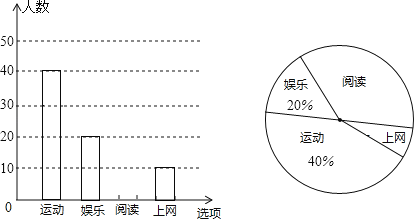
��1��������о��У�һ���������� ��ѧ��������У����![]() ��ѧ��������ȫУ�����˶���ѧ�������� ������
��ѧ��������ȫУ�����˶���ѧ�������� ������
��2����ȫ����ͳ��ͼ���������Ķ�����Բ�Ľ����� ����
��3����ȫУͬѧ�����ѡ��һ��ѧ���μ��ݽ���������Ƶ�ʹ��Ƹ��ʣ���ѡ����ǡ���ǰ����Ķ���ѧ���������� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com