
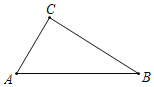
【题目】如图,已知等边![]() 的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线
的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线![]() 是经过点P的一条直线,把
是经过点P的一条直线,把![]() 沿直线
沿直线![]() 折叠,点B的对应点是点
折叠,点B的对应点是点![]() .
.
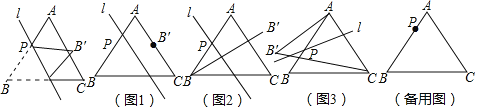
(1)如图1,当![]() 时,若点
时,若点![]() 恰好在AC边上,则
恰好在AC边上,则![]() 的长度为 ;
的长度为 ;
(2)如图2,当![]() 时,若直线
时,若直线![]() ,则
,则![]() 的长度为 ;
的长度为 ;
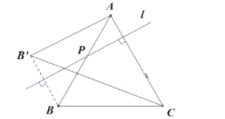
(3)如图3,点P在AB边上运动过程中,若直线![]() 始终垂直于AC,
始终垂直于AC,![]() 的面积是否变化?若变化,说明理由;若不变化,求出面积;
的面积是否变化?若变化,说明理由;若不变化,求出面积;
(4)当![]() 时,在直线
时,在直线![]() 变化过程中,求
变化过程中,求![]() 面积的最大值.
面积的最大值.
【答案】(1)长度为4;(2)长度为5![]() ;(3)△
;(3)△![]() 的面积不变化为16
的面积不变化为16![]() ,理由见解析;(4)△
,理由见解析;(4)△![]() 的面积的最大值为24+4
的面积的最大值为24+4![]() ,理由见解析.
,理由见解析.
【解析】
(1)连接![]() ,由于折叠则△
,由于折叠则△![]() 为等边三角形,即可求出
为等边三角形,即可求出![]() 的长度;(2)记
的长度;(2)记![]() 与BC交于点D,连接
与BC交于点D,连接![]() 和
和![]() ,△BPD和△
,△BPD和△![]() 为边长等于5的等边三角形,所以
为边长等于5的等边三角形,所以![]() 为两边长为5的等边三角形的高之和,求出即可;(3)因为
为两边长为5的等边三角形的高之和,求出即可;(3)因为![]() ⊥AC,
⊥AC, ![]() ∥
∥![]() ,则
,则![]() 到AC的距离始终等于B到AC的距离(平行线之间的距离处处相等),
到AC的距离始终等于B到AC的距离(平行线之间的距离处处相等),![]() 的面积和△ABC的面积相等,算出即可;(4)由题意知
的面积和△ABC的面积相等,算出即可;(4)由题意知![]() =PB=6,所以
=PB=6,所以![]() 始终在以P点为圆心,6为半径的圆上运动,要使得△
始终在以P点为圆心,6为半径的圆上运动,要使得△![]() 面积最大,只要AC边上的高
面积最大,只要AC边上的高![]() 最大,如图,当
最大,如图,当![]() 经过圆心P时,
经过圆心P时,![]() 最大,算出其面积即可.
最大,算出其面积即可.
(1)连接![]() ,
,
∵等边![]() 的边长为8,PB=4,
的边长为8,PB=4,
∴AP=![]() =4,∠PAC=60°,
=4,∠PAC=60°,
∴△![]() 为等边三角形,
为等边三角形,
∴![]() =4;
=4;
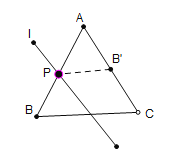
(2)记![]() 与BC交于点D,连接
与BC交于点D,连接![]() 和
和![]() ,
,
∵![]() ∥BC,
∥BC,![]() =BP=5,
=BP=5,
∴△BPD为边长等于5的等边三角形,
所以PD=![]() =5,∠
=5,∠![]() =∠BPD=60°,
=∠BPD=60°,
∴△![]() 为边长等于5的等边三角形,
为边长等于5的等边三角形,
由折叠知![]() ⊥
⊥![]() ,
,
∴![]() 为两边长为5的等边三角形的高之和,
为两边长为5的等边三角形的高之和,
则![]() =
=![]() ;
;

(3)△![]() 的面积不变化,理由如下:
的面积不变化,理由如下:
∵![]() ⊥AC,
⊥AC, ![]() ∥
∥![]() ,
,
∴![]() 到AC的距离始终等于B到AC的距离(平行线之间的距离处处相等),
到AC的距离始终等于B到AC的距离(平行线之间的距离处处相等),
∴S△ACB’=S△ABC=![]() ×82=
×82=![]() ;
;
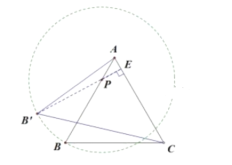
(4)由题意知![]() =PB=6,所以
=PB=6,所以![]() 始终在以P点为圆心,6为半径的圆上运动,要使得△
始终在以P点为圆心,6为半径的圆上运动,要使得△![]() 面积最大,只要AC边上的高
面积最大,只要AC边上的高![]() 最大,如图,当
最大,如图,当![]() 经过圆心P时
经过圆心P时![]() 最大,
最大,
∵∠BAC=60°,
∴AE=![]() AP=1,PE=
AP=1,PE=![]() AE=
AE=![]() ,
,![]() =
=![]() +6,
+6,
此时S△ACB’的最大值为![]() ×AC×
×AC×![]() =
=![]() ×8×(
×8×(![]() +6)=
+6)=![]() +24
+24


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】尺规作图与说理(要求保留作图痕迹,不写作法.)如图,在Rt△ABC中,∠ACB=90°
(1)过点C作AB的垂线CD,交AB于点D;
(2)作∠ABC的平分线BE交AC于点E,交CD于点F;
(3)观察线段CE与CF有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 在
在![]() 上过点
上过点![]() 分别作
分别作![]() 、
、![]() 的平行线,分别交
的平行线,分别交![]() 、
、![]() 于点
于点![]() 、
、![]()
①如果要得到矩形![]() ,那么
,那么![]() 应具备条件:________;
应具备条件:________;
②如果要得到菱形![]() ,那么
,那么![]() 应具备条件:________.
应具备条件:________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点O是边AC上一个动点,过点O作直线
中,点O是边AC上一个动点,过点O作直线![]() //BC,分别交
//BC,分别交![]() ,外角
,外角![]() 的平分线于点E、F.
的平分线于点E、F.

(1)猜想与证明,试猜想线段OE与OF的数量关系,并说明理由.
(2)连接AE,AF,问:当点O在边AC上运动时到什么位置时,四边形AECF是矩形?并说明理由.
(3)若AC边上存在一点O,使四边形AECF是正方形,猜想![]() 的形状并证明你的结论.
的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的一个动点,正方形
边上的一个动点,正方形![]() 是一个边长为
是一个边长为![]() 的动正方形,其中
的动正方形,其中![]() 点在
点在![]() 上,
上,![]() ,(
,(![]() 与
与![]() 分居
分居![]() 的两侧),正方形
的两侧),正方形![]() 与
与![]() 的重叠的面积为
的重叠的面积为![]() .
.
![]() 当
当![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
![]() 当
当![]() 不在
不在![]() 上时,求
上时,求![]() 与
与![]() 的关系式;
的关系式;
![]() 求
求![]() 的最大值.
的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com