
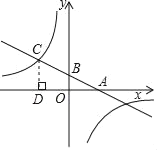
【题目】如图,已知一次函数y=ax+b(a,b为常数,a≠0)的图象与x轴,y轴分别交于点A,B,且与反比例函数y=![]() (k为常数,k≠0)的图象在第二象限内交于点C,作CD⊥x轴于,若OA=OD=
(k为常数,k≠0)的图象在第二象限内交于点C,作CD⊥x轴于,若OA=OD=![]() OB=3.
OB=3.
(1)求一次函数与反比例函数的解析式;
(2)观察图象直接写出不等式0<ax+b≤![]() 的解集.
的解集.
【答案】(1)![]() ,
,![]() ;(2)﹣3≤x<0
;(2)﹣3≤x<0
【解析】
(1)根据已知条件,结合平行线的性质得到CD=2OB=8,又因为OA=OD=![]() OB=3,可求得A(3,0),B(0,4),C(﹣3,8),再利用待定系数求一次函数与反比例函数的解析式即可;(2)根据C点的坐标为(﹣3,8),结合图象找到满足条件x的取值范围即可.
OB=3,可求得A(3,0),B(0,4),C(﹣3,8),再利用待定系数求一次函数与反比例函数的解析式即可;(2)根据C点的坐标为(﹣3,8),结合图象找到满足条件x的取值范围即可.
(1)∵CD⊥OA,
∴DC∥OB,
∴![]() ,
,
∴CD=2OB=8,
∵OA=OD=![]() OB=3,
OB=3,
∴A(3,0),B(0,4),C(﹣3,8),
把A、B两点的坐标分别代入y=ax+b可得![]() ,
,
解得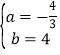 ,
,
∴一次函数解析式为![]() ,
,
∵反比例函数y=![]() 的图象经过点C,
的图象经过点C,
∴k=﹣24,
∴反比例函数的解析式为![]() ;
;
(2)由题意可知所求不等式的解集即为直线AC在x轴上方且在反比例函数图象下方的图象所对应的自变量的取值范围,即线段BC(包含C点,不包含B点)所对应的自变量x的取值范围,
∵C(﹣3,8),
∴0<﹣![]() x+4≤﹣
x+4≤﹣![]() 的解集为﹣3≤x<0.
的解集为﹣3≤x<0.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,连接AC,将![]() 绕点A逆时针旋转α得
绕点A逆时针旋转α得![]() ,连接CF,O为CF的中点,连接OE,OD.
,连接CF,O为CF的中点,连接OE,OD.
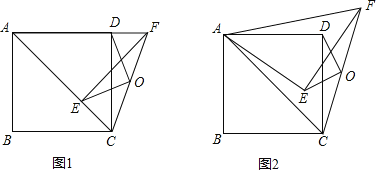
(1)如图1,当![]() 时,请直接写出OE与OD的关系(不用证明).
时,请直接写出OE与OD的关系(不用证明).
(2)如图2,当![]() 时,(1)中的结论是否成立?请说明理由.
时,(1)中的结论是否成立?请说明理由.
(3)当![]() 时,若
时,若![]() ,请直接写出点O经过的路径长.
,请直接写出点O经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是边长为1的正方形ABCD的对角线BD上一动点,点E从点B向点D运动(与点B,D不重合),过点E作直线GH∥BC,交AB于点G,交CD于点H,EF⊥AE,交CD(或CD的延长线)于点F.
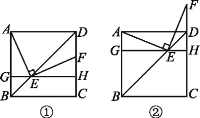
(1)如图①,求证:△AGE≌△EHF.
(2)在点E的运动过程中(如图①,②),四边形AFHG的面积是否会发生变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 在以上4个结论中,正确的有( )
在以上4个结论中,正确的有( )
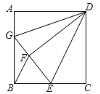
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课中,小张为了测量校园内旗杆AB的高度,站在教学楼的顶端C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°,已知旗杆与教学楼的水平距离CD为10m.
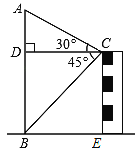
(1)直接写出教学楼CE的高度;
(2)求旗杆AB的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,⊙O过AC的中点D,DE切⊙O于点D,交BC于E.
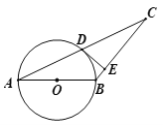
(1)求证DE⊥BC;
(2)若⊙O的半径为5,BE=2,求DE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com