练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在数学活动课中，小张为了测量校园内旗杆AB的高度，站在教学楼的顶端C处测得旗杆底端B的俯角为45°，测得旗杆顶端A的仰角为30°，已知旗杆与教学楼的水平距离CD为10m.

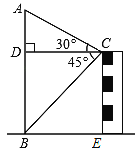
    （1）直接写出教学楼CE的高度；

    （2）求旗杆AB的高度.（结果保留根号）

    【答案】（1）10；（2）.

    【解析】

    试题（1）过点C作CD⊥AB后，图中将有两个直角三角形．先在△BCD中，利用已知角的正切值求出CD，即可求出CE的长；

    （2）然后在△CDA中，利用已知角的正切值求出AD即可解决问题．

    试题解析：（1）CE=10（m）；

    （2）在Rt△ACD中，

    ∵tan∠ACD=，∴=（m），

    在Rt△BCD中，∵tan∠BCD=，

    ∴==10（m），

    ∴AB=AD+BD=（m）．

    考点: 解直角三角形的应用-仰角俯角问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC内接与⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于AC点E，交PC于点F，连接AF．

    （1）判断AF与⊙O的位置关系并说明理由；

    （2）若⊙O的半径为4，AF=3，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

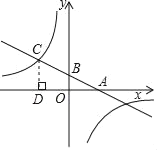
    【题目】如图，已知一次函数y＝ax+b（a，b为常数，a≠0）的图象与x轴，y轴分别交于点A，B，且与反比例函数y＝（k为常数，k≠0）的图象在第二象限内交于点C，作CD⊥x轴于，若OA＝OD＝OB＝3．

    （1）求一次函数与反比例函数的解析式；

    （2）观察图象直接写出不等式0＜ax+b≤的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读以下材料：

    对数的创始人是苏格兰数学家纳皮尔（J. Nplcr，1550-1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evlcr，1707-1783年）才发现指数与对数之间的联系.

    对数的定义：一般地，若，那么叫做以为底的对数，记作：.比如指数式可以转化为，对数式可以转化为.

    我们根据对数的定义可得到对数的一个性质：；理由如下：

    设，，则，

    ∴，由对数的定义得

    又∵

    ∴

    解决以下问题：

    （1）将指数转化为对数式______；

    （2）证明

    （3）拓展运用：计算______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

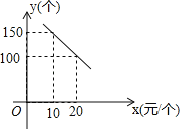
    【题目】某旅游风景区出售一种纪念品，该纪念品的成本为元/个，这种纪念品的销售价格为（元/个）与每天的销售数量（个）之间的函数关系如图所示．

    （1）求与之间的函数关系式；

    （2）销售价格定为多少时，每天可以获得最大利润？并求出最大利润．

    （3）“十一”期间，游客数量大幅增加，若按八折促销该纪念品，预计每天的销售数量可增加，为获得最大利润，“十一”假期该纪念品打八折后售价为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某建筑物，从10m高的窗口A，用水管向外喷水，喷出的水呈抛物线状（抛物线所在的平面与墙面垂直），如图所示，如果抛物线的最高点M离墙1m，离地面m，则水流落地点B离墙的距离OB是（ ）

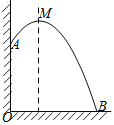
    A.2mB.3mC.4mD.5m

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司生产的商品的市场指导价为每件150元，公司的实际销售价格可以浮动x个百分点（即销售价格＝150（1+x%）），经过市场调研发现，这种商品的日销售量y（件）与销售价格浮动的百分点x之间的函数关系为y＝﹣2x+24．若该公司按浮动﹣12个百分点的价格出售，每件商品仍可获利10%．

    （1）求该公司生产销售每件商品的成本为多少元？

    （2）当实际销售价格定为多少元时，日销售利润为660元？（说明：日销售利润＝（销售价格一成本）×日销售量）

    （3）该公司决定每销售一件商品就捐赠a元利润（a≥1）给希望工程，公司通过销售记录发现，当价格浮动的百分点大于﹣2时，扣除捐赠后的日销售利润随x增大而减小，直接写出a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

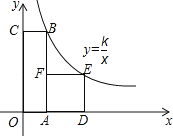
    【题目】如图，四边形OABC是矩形，ADEF是正方形，点A、D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B，E在反比例函数y＝的图象上，OA＝1，OC＝6，试求出正方形ADEF的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上，过点C作CD⊥AB，分别交AB、AO的延长线于点D、E，AE交半圆O于点F，连接CF.

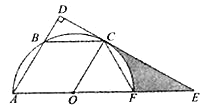
    （1）判断直线DE与半圆O的位置关系，并说明理由；

    （2）若半圆O的半径为12，求涂色部分的周长.

    查看答案和解析>>

    同步练习册答案