
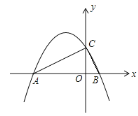
【题目】如图,二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于点C,若AC⊥BC,则a的值为_______.
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有 (写出所有正确结论的序号)
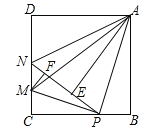
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为![]() ;
;
⑤当△ABP≌△ADN时,BP=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年2月16日,由著名导演林超贤的电影《红海行动》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用摸球的办法决定谁去看电影,规则如下:在一个不透明的袋子中装有编号1~4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.
(1)请用列表或画树状图的方法表示出两数和的所有可能的结果;
(2)分别求出小亮和小丽获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
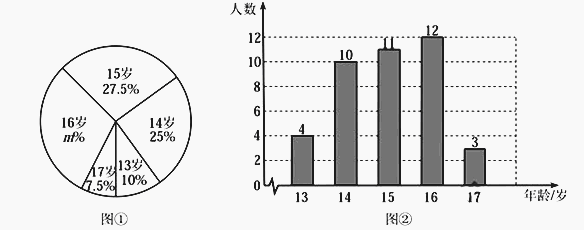
(1)本次接受调查的跳水运动员人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 x1、x2是一元二次方程4kx2﹣4kx+k+1=0的两个实数根.
(1)求k的取值范围.
(2)是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣![]() 成立?若存在求出k的值;若不存在,请说明理由.
成立?若存在求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长沙市马王堆蔬菜批发市场某批发商原计划以每千克10元的单价对外批发销售某种蔬菜![]() 为了加快销售,该批发商对价格进行两次下调后,售价降为每千克
为了加快销售,该批发商对价格进行两次下调后,售价降为每千克![]() 元.
元.
![]() 求平均每次下调的百分率;
求平均每次下调的百分率;
![]() 某大型超市准备到该批发商处购买2吨该蔬菜,因数量较多,该批发商决定再给予两种优惠方案以供选择
某大型超市准备到该批发商处购买2吨该蔬菜,因数量较多,该批发商决定再给予两种优惠方案以供选择![]() 方案一:打八折销售;方案二:不打折,每吨优惠现金1000元
方案一:打八折销售;方案二:不打折,每吨优惠现金1000元![]() 试问超市采购员选择哪种方案更优惠?请说明理由.
试问超市采购员选择哪种方案更优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
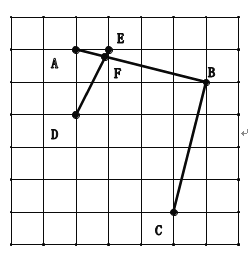
【题目】如图,在每个小正方形的边长为1的网格中,取格点A、B、C并连接AB,BC.取格点D、E并连接,交AB于点F.
(Ⅰ)BF的长等于_____;
(Ⅱ)若点G在线段BC上,且满足AF+CG=FG,请在如图所示的网格中,用无刻度的直尺,确定点G的位置,并简要说明点G的位置是如何找到的________________________________________(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
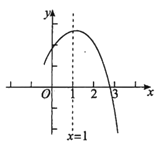
【题目】如图是二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )图象的一部分,与
)图象的一部分,与![]() 轴的交点
轴的交点![]() 在点
在点![]() 和
和![]() 之间,对称轴是
之间,对称轴是![]() .有下列说法:①
.有下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤当
为实数);⑤当![]() 时,
时,![]() .其中正确的是______(填写所有正确结论的序号).
.其中正确的是______(填写所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形四边形ABCD中,![]() ,
,![]() ,对角线AC、BD交于点O,点P为直线BD上的动点
,对角线AC、BD交于点O,点P为直线BD上的动点![]() 不与点B重合
不与点B重合![]() ,连接AP,将线段AP绕点P逆时针旋转
,连接AP,将线段AP绕点P逆时针旋转![]() 得到线段PE,连接CE、BE.
得到线段PE,连接CE、BE.
![]() 问题发现
问题发现
如图1,当点E在直线BD上时,线段BP与CE的数量关系为______;![]() ______
______![]()
![]() 拓展探究
拓展探究
如图2,当点P在线段BO延长线上时,![]() 的结论是否成立?若成立,请加以证明;若不成立,请说明理由;
的结论是否成立?若成立,请加以证明;若不成立,请说明理由;
![]() 问题解决
问题解决
当![]() 时,请直接写出线段AP的长度.
时,请直接写出线段AP的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com