
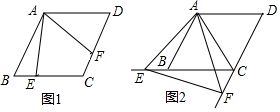
分析 (1)欲证明BE=CF,只要证明△BAE≌△CAF即可.
(2)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,根据FH=CF•cos30°,因为CF=BE,只要求出BE即可解决问题.
解答 (1)证明:连接AC,如图1中,∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAE,
在△BAE和△CAF中,
$\left\{\begin{array}{l}{∠BAE=∠CAF}\\{BA=AC}\\{∠B=∠ACF}\end{array}\right.$,
∴△BAE≌△CAF,
∴BE=CF.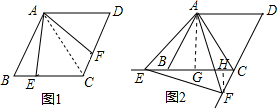
(2)解:如图2中,过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,
∵∠EAB=15°,∠ABC=60°,
∴∠AEB=45°,
在RT△AGB中,∵∠ABC=60°,AB=4,
∴BG=$\frac{1}{2}$AB=2,AG=$\sqrt{3}$BG=2 $\sqrt{3}$,
在RT△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2 $\sqrt{3}$,
∴EB=EG-BG=2 $\sqrt{3}$-2,
∵△AEB≌△AFC,
∴AE=AF,EB=CF=2 $\sqrt{3}$-2,
在RT△CHF中,∵∠HCF=180°-∠BCD=60°,CF=2 $\sqrt{3}$-2,
∴FH=CF•sin60°=(2 $\sqrt{3}$-2)•$\frac{\sqrt{3}}{2}$=3-$\sqrt{3}$.
∴点F到BC的距离为3-$\sqrt{3}$.
点评 本题考查四边形综合题、菱形的性质、等边三角形的判定、全等三角形的判定和性质等知识,解题的关键是灵活应用这些知识解决问题,学会添加常用辅助线,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )| A. | mn | B. | $\frac{1}{2}$mn | C. | $\frac{1}{4}$mn | D. | $\sqrt{mn}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,$\frac{AB′}{AB}$=$\frac{B′C′}{BC}$=$\frac{AC′}{AC}$=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ=72°,n=$\frac{1+\sqrt{5}}{2}$.
把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,$\frac{AB′}{AB}$=$\frac{B′C′}{BC}$=$\frac{AC′}{AC}$=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ=72°,n=$\frac{1+\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
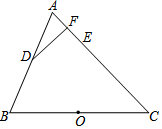 如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.
如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.
如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
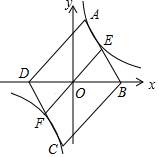 如图,点B,D分别在x轴的正、负半轴上,OB=OD,以BD为对角线作?ABCD,使点A、C分别落在反比例函数y=$\frac{k}{x}$的第一、三象限的图象上,且S?ABCD=28.AB、CD分别交反比例图象于点E、F,连结EF.当四边形BEFC是平行四边形时,k的值是$\frac{14}{3}$.
如图,点B,D分别在x轴的正、负半轴上,OB=OD,以BD为对角线作?ABCD,使点A、C分别落在反比例函数y=$\frac{k}{x}$的第一、三象限的图象上,且S?ABCD=28.AB、CD分别交反比例图象于点E、F,连结EF.当四边形BEFC是平行四边形时,k的值是$\frac{14}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
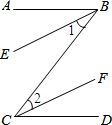 (1)完成下面的推理说明:
(1)完成下面的推理说明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com