
 把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,$\frac{AB′}{AB}$=$\frac{B′C′}{BC}$=$\frac{AC′}{AC}$=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ=72°,n=$\frac{1+\sqrt{5}}{2}$.
把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,$\frac{AB′}{AB}$=$\frac{B′C′}{BC}$=$\frac{AC′}{AC}$=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ=72°,n=$\frac{1+\sqrt{5}}{2}$. 分析 由四边形ABB′C′是平行四边形,易求得θ=∠CAC′=∠ACB=72°,又由△ABC∽△B′BA,根据相似三角形的对应边成比例,易得AB2=CB•BB′=CB(BC+CB′),继而求得答案.
解答 解:∵四边形ABB′C′是平行四边形,
∴AC′∥BB′,
又∵∠BAC=36°,
∴θ=∠CAC′=∠ACB=72°,
∴∠C′AB′=∠ABB′=∠BAC=36°,而∠B=∠B,
∴△ABC∽△B′BA,
∴AB2=CB•B′B=CB•(BC+CB′),而CB′=AC=AB=B′C′,BC=1,
∴AB2=1•(1+AB),
∴AB=$\frac{1±\sqrt{5}}{2}$,
∵AB>0,
∴n=$\frac{B′C′}{BC}$=$\frac{1+\sqrt{5}}{2}$.
故答案为:72°,$\frac{1+\sqrt{5}}{2}$.
点评 此题考查了相似三角形的判定与性质、旋转的性质以及平行四边形的性质,注意数形结合思想与方程思想的应用.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
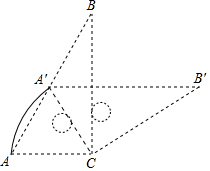 如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )
如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )| A. | πcm | B. | 2πcm | C. | $\frac{8π}{3}cm$ | D. | 4πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
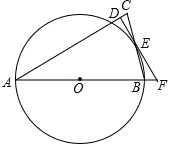 如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作O的切线交AC于点D,且ED⊥AC.
如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作O的切线交AC于点D,且ED⊥AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
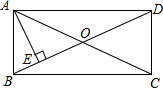 如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.
如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 七巧板被西方人称为“东方魔板”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图a)的边长为4,则“一帆风顺”(如图b)阴影部分的面积为1.
七巧板被西方人称为“东方魔板”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图a)的边长为4,则“一帆风顺”(如图b)阴影部分的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com