
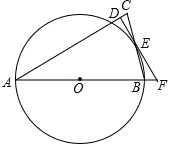
 如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作O的切线交AC于点D,且ED⊥AC.
如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作O的切线交AC于点D,且ED⊥AC.分析 (1)连接OE,AE.只要证明AE⊥BC,EC=BE即可;
(2)作OM⊥AC于M.由四边形OEDM是矩形,推出OE=DM=2,由AD=2+$\sqrt{3}$,推出AM=$\sqrt{3}$,在Rt△AOM中,cosA=$\frac{AM}{OA}$=$\frac{\sqrt{3}}{2}$,推出∠A=30°,在Rt△OEF中,EF=OE•tan30°=$\frac{2\sqrt{3}}{3}$,根据弧BE和BF、EF围成的部分的面积S=S△OEF-S扇形OEB计算即可;
解答 (1)证明:连接OE,AE.
∵DF是⊙O的切线,
∴OE⊥DF,
∵AC⊥DF,
∴OE∥AC,
∵OA=OB,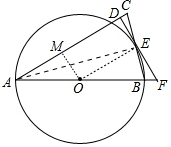
∴EC=EB,
∵AE⊥BC,
∴AC=AB.
(2)解:作OM⊥AC于M.
∵∠OMD=∠MDE=∠OED=90°,
∴四边形OEDM是矩形,
∴OE=DM=2,
∵AD=2+$\sqrt{3}$,
∴AM=$\sqrt{3}$,
在Rt△AOM中,cosA=$\frac{AM}{OA}$=$\frac{\sqrt{3}}{2}$,
∴∠A=30°,
∵OE∥AC,
∴∠EOF=30°,
在Rt△OEF中,EF=OE•tan30°=$\frac{2\sqrt{3}}{3}$,
∴弧BE和BF、EF围成的部分的面积S=S△OEF-S扇形OEB=$\frac{1}{2}$×2×$\frac{2\sqrt{3}}{3}$-$\frac{30•π•2}{180}$=$\frac{2\sqrt{3}}{3}$-$\frac{1}{3}$π.
点评 本题考查切线的性质、扇形的面积公式、矩形的判定等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,属于中考常考题型.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
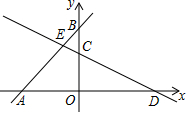 如图,直线y=mx+3与x轴、y轴交于点A、点B,直线CD与x轴交于点D,与y轴交于点C(0,2),与直线AB交于点E,点E的坐标为(-$\frac{2}{3}$,$\frac{7}{3}$).
如图,直线y=mx+3与x轴、y轴交于点A、点B,直线CD与x轴交于点D,与y轴交于点C(0,2),与直线AB交于点E,点E的坐标为(-$\frac{2}{3}$,$\frac{7}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )| A. | mn | B. | $\frac{1}{2}$mn | C. | $\frac{1}{4}$mn | D. | $\sqrt{mn}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,$\frac{AB′}{AB}$=$\frac{B′C′}{BC}$=$\frac{AC′}{AC}$=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ=72°,n=$\frac{1+\sqrt{5}}{2}$.
把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,$\frac{AB′}{AB}$=$\frac{B′C′}{BC}$=$\frac{AC′}{AC}$=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ=72°,n=$\frac{1+\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.
如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
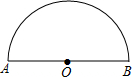 如图,AB是半圆O的直径,且AB=4cm,动点P从点O出发,沿OA→$\widehat{AB}$→BO的路径以每秒1cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )
如图,AB是半圆O的直径,且AB=4cm,动点P从点O出发,沿OA→$\widehat{AB}$→BO的路径以每秒1cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )| A. | 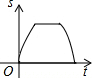 | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com